Control Theory

Proportional Integral Derivative (PID) Control

PID is used everywhere. PID describe how the error term is handled.

This video treats line following as PID for self-driving cars.

Good Lecture Series by Brian Douglas: https://www.youtube.com/playlist?list=PLn8PRpmsu08pQBgjxYFXSsODEF3Jqmm-y

Why make a simpler controller?

1. Easy to implement
2. Easy to test and troubleshoot
3. Easy to understand

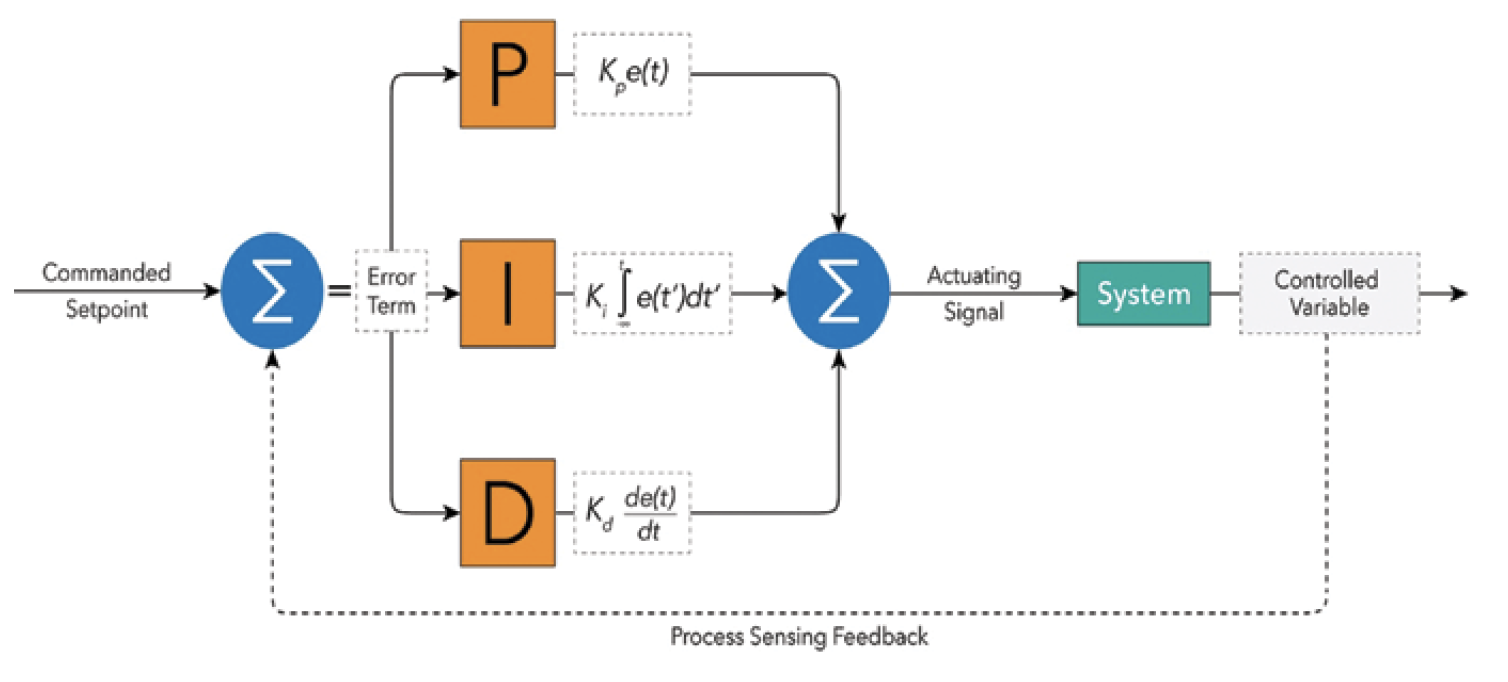
The Equation $u(t)=K_{p}e(t)+K_i{\int }_0^{t}e(t^{\prime })d{t}^{\prime }+K_d\frac{d}{dt}(e(t))$ where

• $u(t)$ is the control output (in our case is the steering angle we want the car to drive at)
• $K_p$,$K_i$ and $K_d$ are constants that determine how much weight each of the three components (proportional, integral, derivative) contribute to the
• $e(t)$ is the error term. This is the difference between the set point and the parameter we want to maintain around that set point.

Implementation in code (at least the super simple way):

• $e(t)$ is the measured error at time $t$
• $\frac{de(t)}{dt}\approx \frac{e_t-e_{t-1}}{\Delta t}$, i.e. take the differences the error between a timestep divided by the time elapsed for a timestep
• $\int e(t)dt\approx \sum e(t)\Delta t$, i.e sum the errors and multiple it by the time elapsed since the beginning measurement.

Other implementation things you need to think about:

• If your PID controller runs for a long time, $\sum e(t)\to \infty$
• Division by very small numbers if you $\Delta t$ is very small

Components of a PID Controller

• Proportional Control: Steering of the car is proportional to the crosstrack error.
• Derivative Control: To avoid overshooting the car and oscillating around the centerline with a simple proportional control, we add derivative control to counterbalance.
• Integral Control: This is to counterbalance the stead-state error over time. The integral control corrects for the total error so far.

Combining all three of these create the PID controller.

PID Tuning

There is a science behind tuning, but the most common method is manual tuning.

• https://www.youtube.com/watch?v=IB1Ir4oCP5k&ab_channel=RealPars

Ziegler-Nichols method is a way to tune, got it from CARLA

This is a really good guide: https://tlk-energy.de/blog-en/practical-pid-tuning-guide

pid