Race Condition

A situation in which multiple threads or processes read and write a shared data item, and the final result depends on the relative timing of their execution.

Concurrency

Race conditions happen when threads run through critical sections without thread synchronization. The threads “race” through the critical section to write or read shared resources and depending on the order in which threads finish the “race”, the program output changes.

In a race condition, threads access shared resources or program variables that might be worked on by other threads at the same time causing the application data to be inconsistent.

How to avoid race conditions?

These can be avoided with proper thread synchronization within critical sections by using techniques like Lock, Atomic Variables, and message passing.

Example

Suppose two processes, P1 and P2, share the global variable a. At some point in its execution, P1 updates a to the value 1, and at some point in its execution, P2 updates a to the value 2. Thus, the two tasks are in a race to write variable a. In this example, the “loser” of the race (the process that updates last) determines the final value of a.

Example

P1:
    a = a + 1;
    b = b + 1;
P2:
    b = 2 * b;
    a = 2 * a;

From ECE124

Race Condition exists when 2 or more state variables change value at the same time in response to a change in the value of a circuit input.

When unequal delays are encountered, a race condition may cause the state variable to change in an unpredictable manner.

I also saw Data Race in ECE222.

Two types of Races

Assume two state variables change…

• If circuit reaches the same final stable-state regardless of order of state variable changes, then it is a non-critical race
• If circuit reaches different final stable-state based on order of state variable changes, then it is a critical race

Why Races Exist

Races are a consequence of how states are assigned when designing a circuit. They exist in transition tables, but not in flow tables.

Flow Tables are entirely symbolic, there’s no underlying circuitry logic, so we don’t see the problems there. Transition Tables have binary values present, so potential problems there.

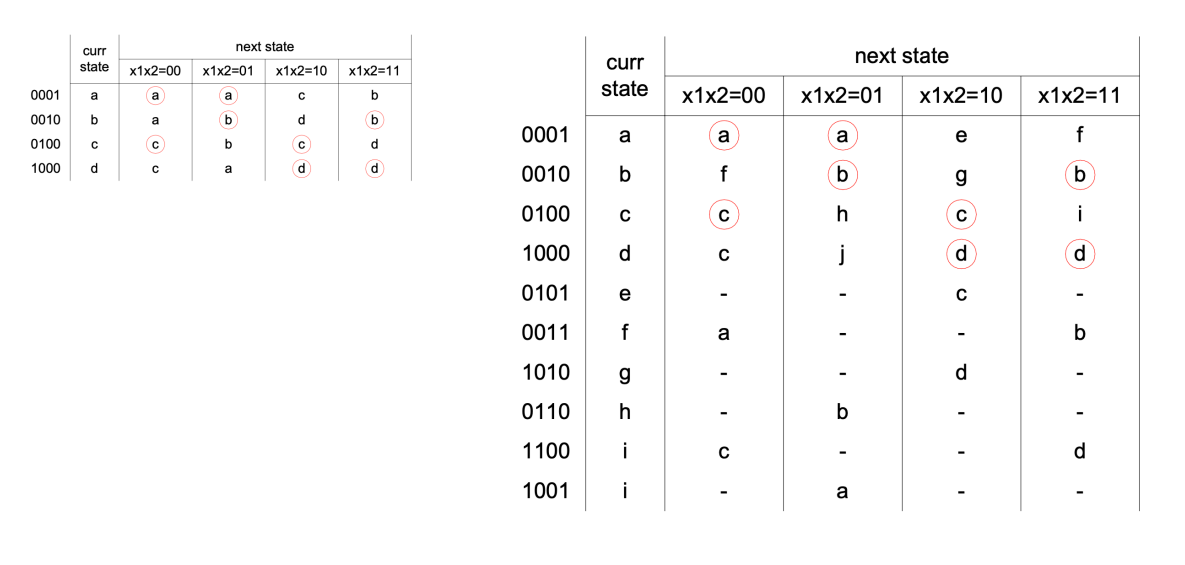
Three Methods for Race Free State Assignment

Method 1: Use a 3D Cube Method 2: Use equivalent states, i.e. A1, A2, B1, B2, etc. Method 3: One Hot Encode

1 at ith position For the additional sates, transition from ith state to j-th state, introduce unstable encoding with 1’s in ith and jth position

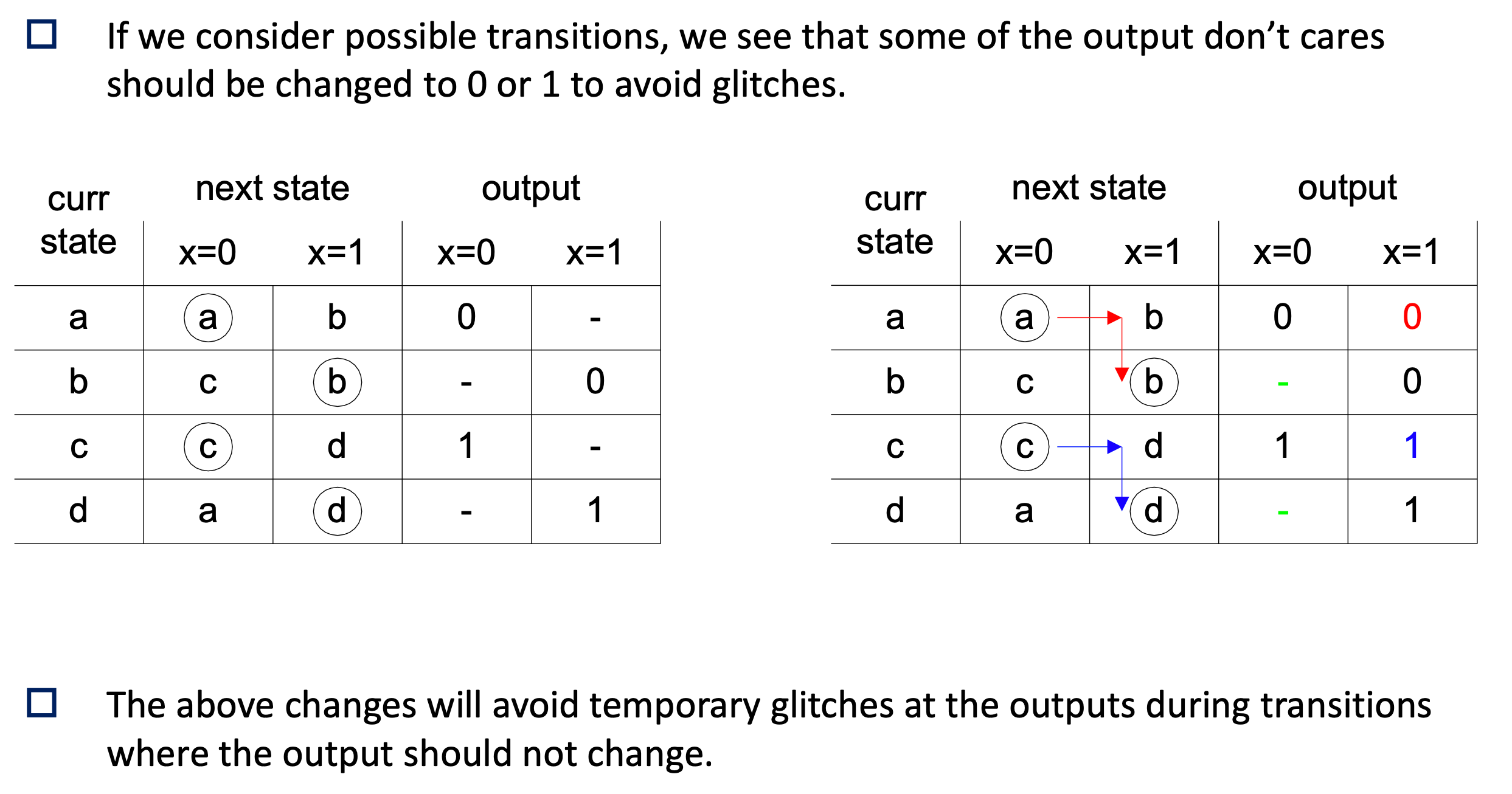
Avoiding Output glitches

Basically, once you reach the final table, you gotta look at the don’t care’s of the stable states

• If both stable states produce the same output (0 or 1), (IMPORTANT: the entire row has to be the same value) then make the output directly that value instead of a don’t care
• Else, if you see there are different output values, leave it as a don’t care