Heap

A heap refers to the heap tree-shaped data structured used in to implement a Priority Queue.

Do confused this with the Heap (Memory). There is no connection between them.

Resources

• https://www.programiz.com/dsa/heap-data-structure

Binary Heap

A Binary Heap is another way of implementing a Priority Queue. A binary heap is a heap, i.e, a tree which obeys the heap property: the root of any tree is greater than or equal to (or smaller than or equal to) all its children.

Heap Invariant: for ALL subtrees, root > left child, right child

Heap vs Tree

Heap vs. Self-Balancing Binary Search Tree?

• Because Heap implements the Priority Queue, whereas Self-Balancing Binary Search Tree implements the Ordered Map in C++.

I have trouble seeing the use case of heaps.

• https://stackoverflow.com/questions/6147242/heap-vs-binary-search-tree-bs
• https://www.baeldung.com/cs/heap-vs-binary-search-tree
• https://www.geeksforgeeks.org/difference-between-binary-search-tree-and-binary-heap/

Heap time complexities

• Get min: $O(1)$
• Insertion: $O(\log n)$ (since you need to do a fix-up)
• Delete-min: $O(\log n)$ (since you need to do a fix-down)

Why would you use Heap over BST?

The killer feature of heaps is that average time insertion into a binary heap is $O(1)$, for BST is $O(\log (n))$.

Heaps are great to get the minimum or the maximum value in $O(1)$. However, if you want to search for a particular key, you are better off using a BST.

CS240

When inserting a heap, you always need to put it in the left-most. Then, you do a swap operation. Since there are at most $O(\log n)$ levels, the insertion takes $O(\log n)$ time.

We take the child with the larger key

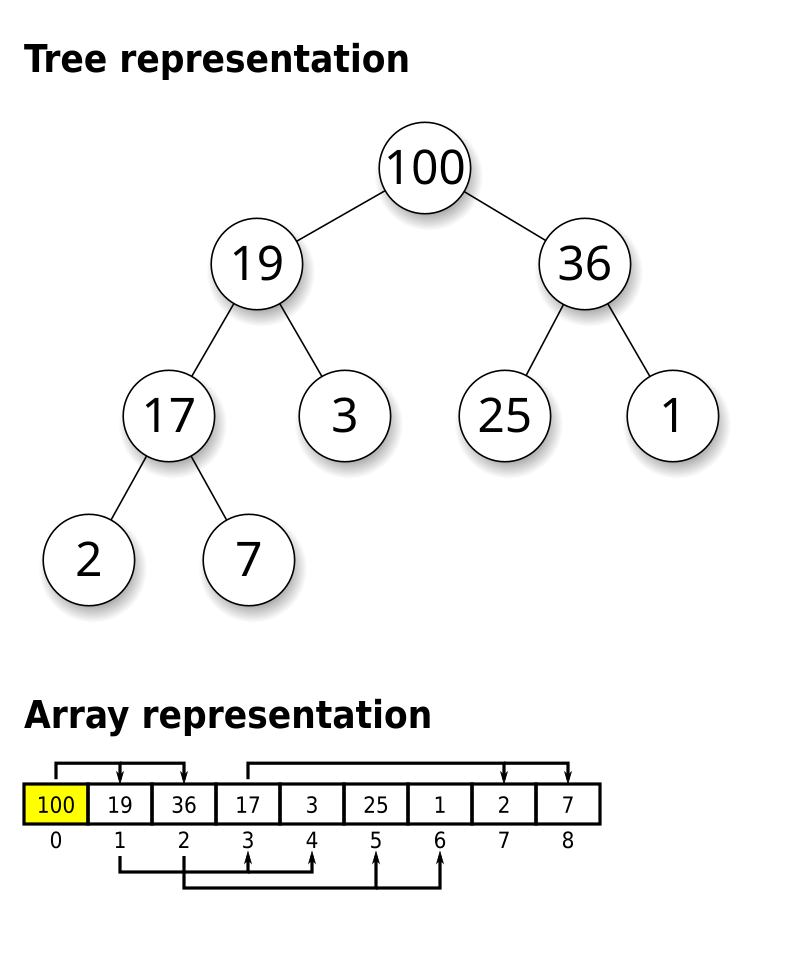
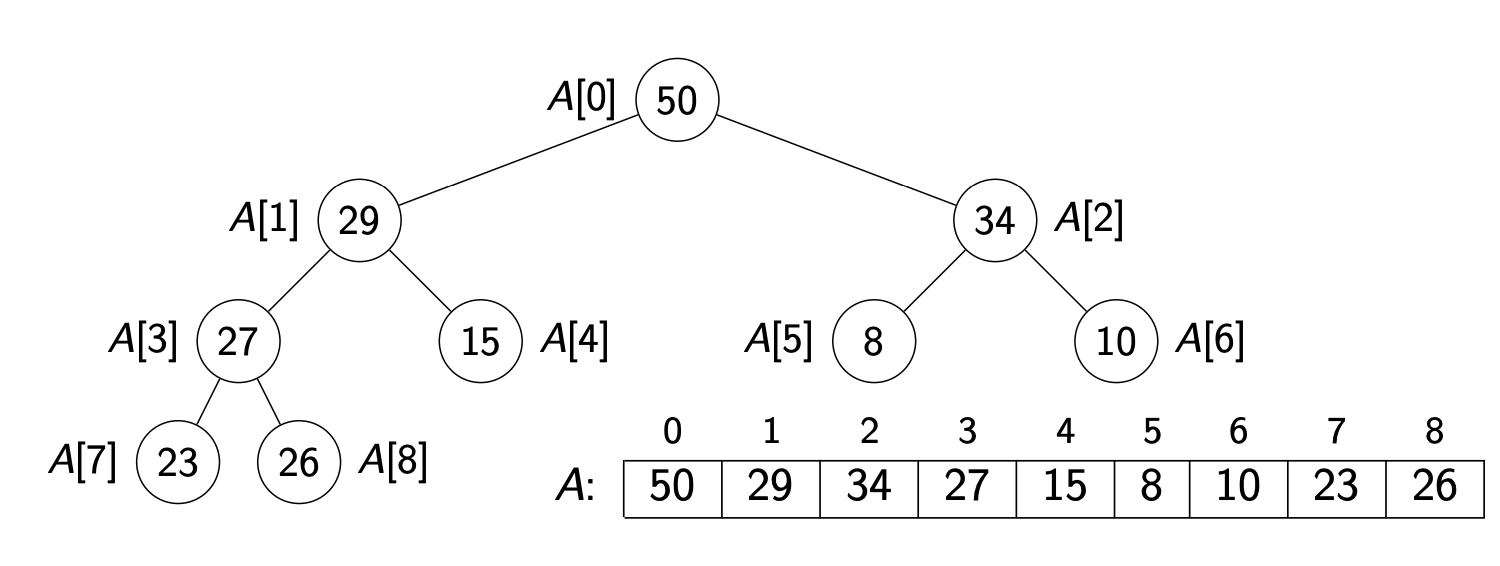
Storing Heaps in Arrays

Heaps should not be stored as binary trees! Let H be a heap of n items and let A be an array of size n. Store root in $A[0]$ and continue with elements level-by-level from top to bottom, in each level left-to-right

This is exactly how we encode it in a Segment Tree! (except we use 1-index?)

It is easy to navigate the heap using this array representation:

• the root node is at index 0 (We use “node” and “index” interchangeably in this implementation.)
• the last node is $n-1$ (where n is the size)
• the left child of node i (if it exists) is node $2i+1$
• the right child of node i (if it exists) is node $2i+2$
• the parent of node i (if it exists) is node $\lfloor \frac{i-1}{2}\rfloor$
• these nodes exist if the index falls in the range $\{0,...,n-1\}$

In practice, use 1-indexing

It is more convenient to use 1-indexing. See Segment Tree for how this is implemented.

The Priority Queue uses the heap. In C++, the underlying implementation is a C++ Vector.

Problems

The problem that you struggle the most is implementing the LRU scheme using a heap.

Basically, have a table that stores the latest time. And as you pop from the heap, make sure that is the latest, else it doesn’t count.

Related

• Heap Sort