Series

Infinite series

An infinite series (or just series) of constants $a_k$ is defined as a limit of finite series: ${\sum }_{k=0}^{\infty }{a}_k={\lim }_{n\to \infty }{\sum }_{k=0}^n{a}_k$

Geometric Series

A geometric series can be written in the form ${\sum }_{k=0}^{\infty }a{r}^k=a+ar+a{r}^2+a{r}^3+\dots$ The sum of Geometric series is given by $S_n=\frac{a(1-r^{n+1})}{1-r}$

new kind of series from CS370

Doesn’t have to sum to infinity ${\sum }_{j=0}^{N-1}{x}^j=\frac{x^N-1}{x-1}$ where $x\ne 1$

• Applying this for example to compute the number of nodes in a tree, ${\sum }_{i=0}^{N-1}{2}^i=2^N-1$

Telescoping Series

a telescoping series is a series whose general term can be written as the difference of two consecutive terms of a sequence, i.e. $t_n=a_n-a_{n+1}$

Convergence / Divergence Tests

Convergence Test

Used on geometric series. ${\sum }_{k=0}^{\infty }a{r}^k=\frac{a}{1-r}\text{if }|r|<1\text{, and is divergent otherwise.}$

n^{th} Term Test (Test for Divergence)

If ${\lim }_{k\to \infty }{a}_k\ne 0$, then $\sum a_k$ diverges.

DANGER: If ${\lim }_{n\to \infty }{a}_n=0$, we cannot make any conclusions about divergence or convergence.

The Integral Test (Condition to use: all a_k > 0)

Theorem: Consider a series ${\sum }_{k=k_0}^{\infty }{a}_k$. Let $f$ be a function which is continuous, positive, and decreasing on $(k_0,\infty )$, with $f(k)=a_k$ for all $k\ge k_0$.

1. If ${\int }_{k_0}^{\infty }f(x)dx$ converges, then ${\sum }_{k=k_0}^{\infty }{a}_k$ converges.
2. If ${\int }_{k_0}^{\infty }f(x)dx$ diverges, then ${\sum }_{k=k_0}^{\infty }{a}_k$ diverges.

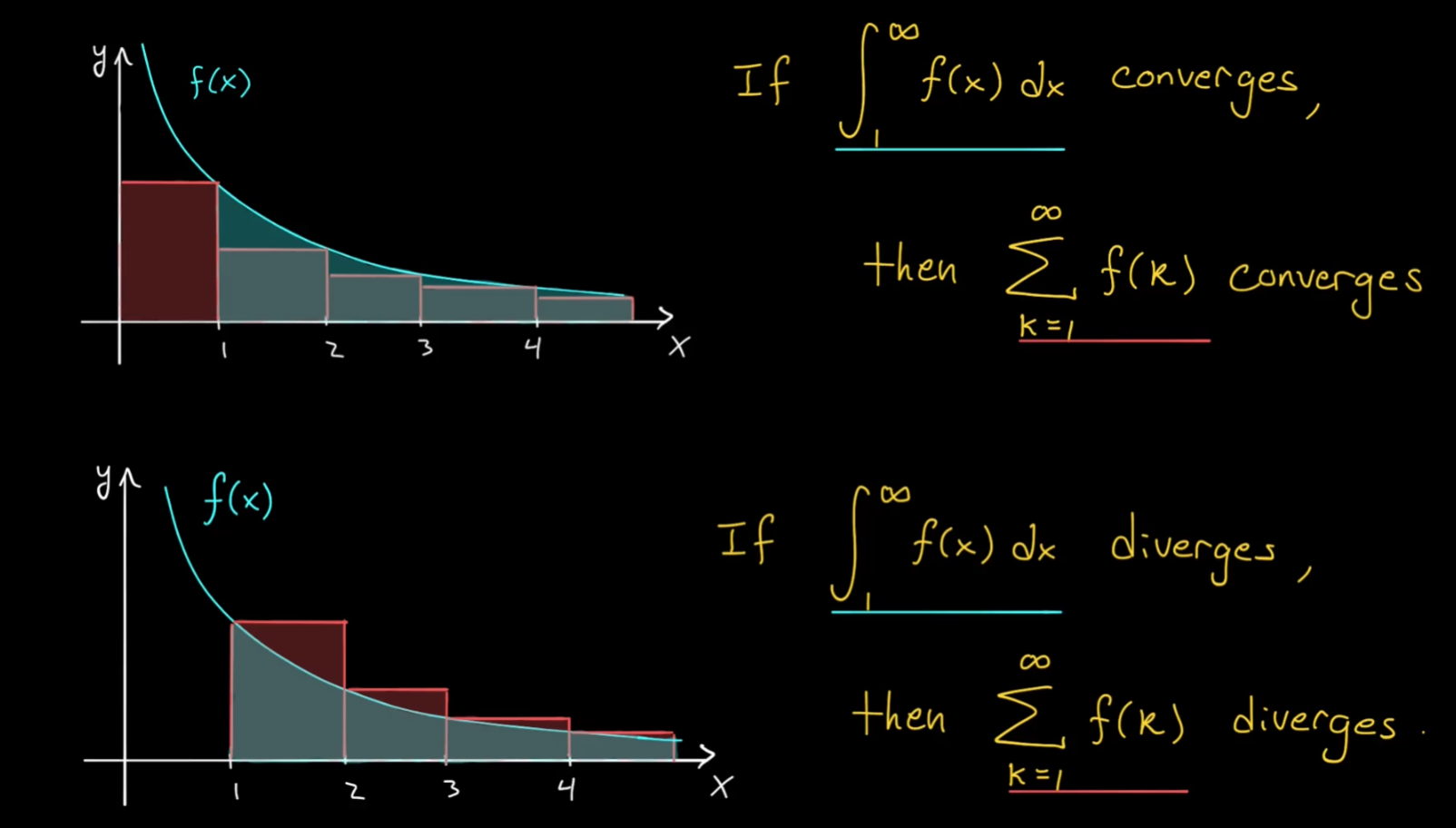
Convergence of P-Series

$\sum \frac{1}{k^p}\text{converges if }p>1,\text{ and diverges if }p\le 1$

Direct Comparison Test (Condition to use: a_k > 0)

Given a positive series $\sum a_k$. If we find another series $\sum b_k$, where

1. $a_k\le b_k$, and if $\sum b_k$ converges, then $\sum a_k$ converges.
2. $a_k\ge b_k$, and if $\sum b_k$ diverges, then $\sum a_k$ diverges.

Limit Comparison Test ( a_k > 0)

Assume that the following limit exists (or $=\infty$): $L={\lim }_{k\to \infty }\frac{a_k}{b_k}$

• If $L=C$ (non-zero constant), then $\sum a_k$ converges $⟺\sum b_k$ converges
  • They either both converge or both diverge
• If $L=0$, and $\sum b_k$ converges, then $\sum a_k$ also converges
• If $L=\infty$, and $\sum b_k$ diverges, then $\sum a_k$ also diverges

Alternating Series Test (AST) / Leibniz Test

Consider the series ${\sum }_{k=0}^{\infty }(-1{)}^k{a}_k$, where $a_k>0$ for every $k$. If

1. $a_k$ is a decreasing sequence, and
2. ${\lim }_{k\to \infty }{a}_k=0$,

then the series converges.

Alternative Series Estimation Theorem (ASET)

Consider the series ${\sum }_{k=0}^{\infty }(-1{)}^k{a}_k$, where $a_k>0$ for every $k$. If

1. $a_k$ is a decreasing sequence, and
2. ${\lim }_{k\to \infty }{a}_k=0$,

Then $|s-s_n|\le a_{n+1}$.

The Ratio Test

Assume that the following limit exists (or $=\infty$): $L={\lim }_{k\to \infty }\left|\frac{a_{k+1}}{a_k}\right|$

• If $L<1$, then $\sum a_k$ is absolutely convergent.
• If $L>1$, then $\sum a_k$ is divergent.
• If $L=1$, then the test fails.

The Root Test

Assume that the following limit exists (or $=\infty$): $L={\lim }_{k\to \infty }\sqrt[k]{|a_k|}$

• If $L<1$, then $\sum a_k$ is absolutely convergent.
• If $L>1$, then $\sum a_k$ is divergent.
• If $L=1$, then the test fails.

Conditional vs. Absolute Convergence

A series $\sum a_k$ is called absolutely convergent if $\sum |a_k|$ converges.

Absolute Convergence Implies Convergence

If the series $\sum |a_k|$ converges, then $\sum a_k$ also converges.

A series $\sum a_k$ is said to be conditionally convergent if it converges, but the series $\sum |a_k|$ diverges.

To check between for absolute convergence, we use The Ratio Test.

Related

• Power Series
• Harmonic Series