Tree

Spanning Tree

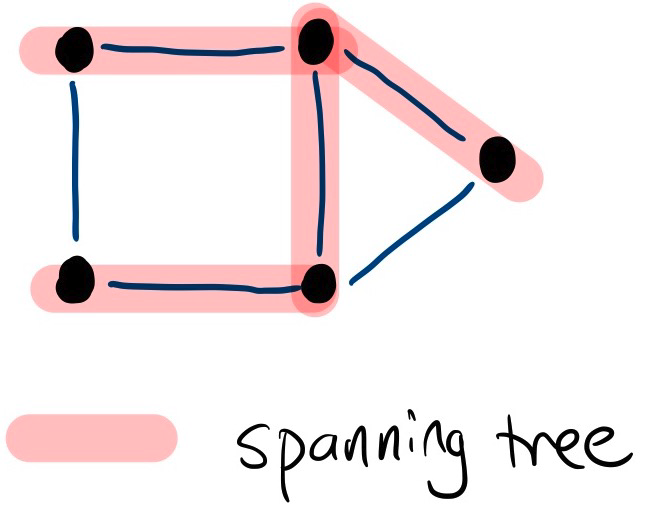
A spanning tree of a graph consists of all nodes of the graph and some of the edges of the graph so that there is a path between any two nodes.

Like trees in general, spanning trees are connected and acyclic. Usually there are several ways to construct a spanning tree.

minimum spanning tree = spanning tree whose weight is as small as possible maximum spanning tree = spanning tree whose weight is as large as possible

You have two options to find the minimum/maximum spanning tree:

• Kruskal’s Algorithm
• Prim’s Algorithm

From MATH239

Spanning Tree

A spanning tree of $G$ is a spanning subgraph of $G$ that is a tree. In other words, $V(T)=V(G),E(T)\subseteq E(G)$, $T$ is a tree.

Theorems and Corollaries

Theorem 5.2.1

A graph $G$ is Connected if and only if $G$ has a spanning tree.

Corollary 5.2.2

If $G$ is a Connected Graph with $n$ vertices and $n-1$ edges, then $G$ is a tree.

Corollary 2

Let $G$ be a graph with $n$ vertices. If any 2 of the following 3 conditions hold, then $G$ is a tree:

1. $G$ is connected
2. $G$ has no cycles
3. $G$ has $n-1$ edges

Theorem 5.2.3

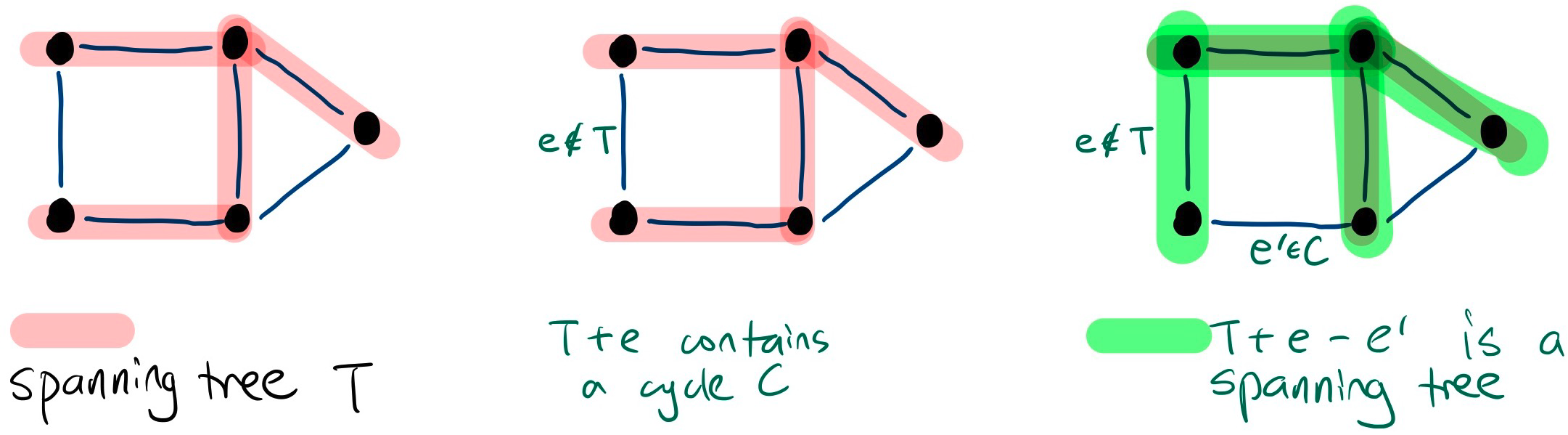
If $T$ is a spanning tree of $G$ and $e\notin E(T)$, then $T+e$ contains exactly one cycle $C$. Moreover, if $e^{\prime }\in E(C)$, then $T+e-e^{\prime }$ is a spanning tree of $G$.

Theorem 5.2.4

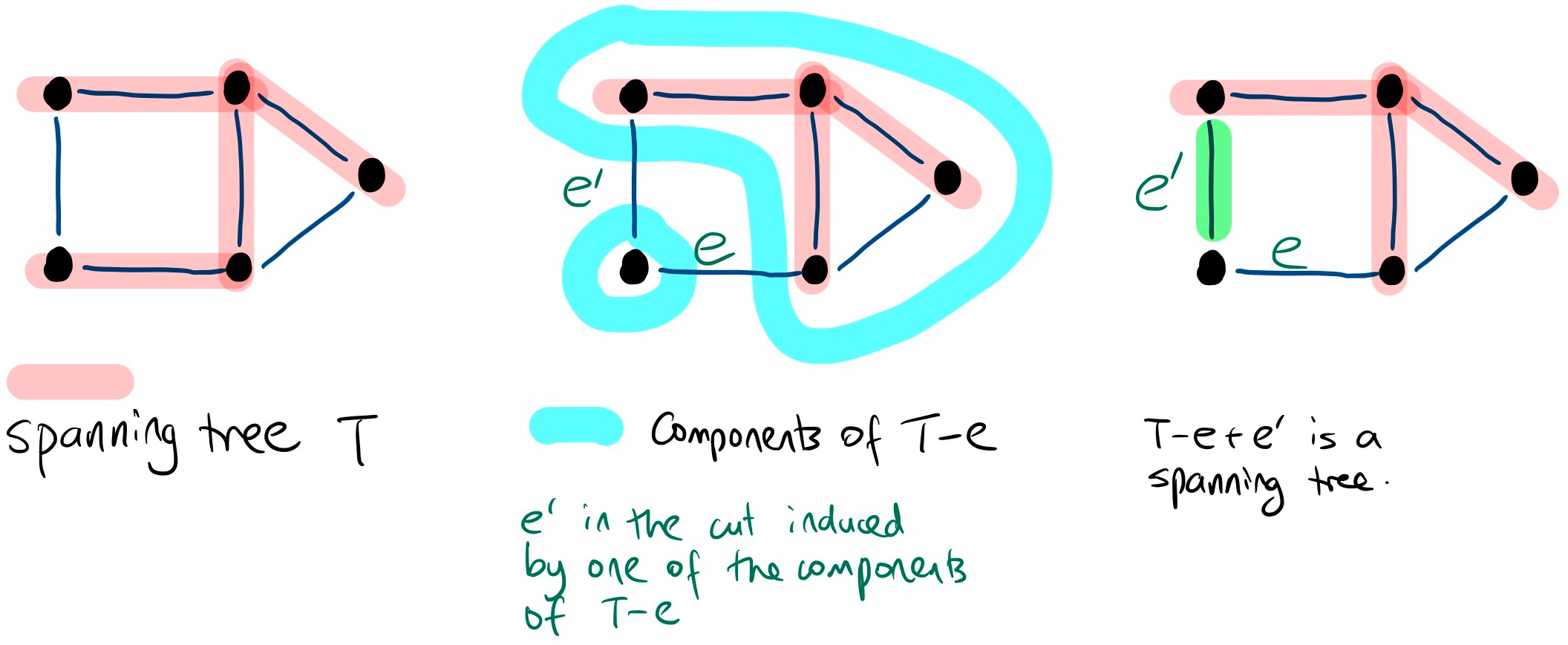
If $G$ is a spanning tree of $G$ and $e\in E(T)$, then $T-e$ has 2 components. If $e^{\prime }$ an edge in the cut induced by the vertices of one component, then $T-e+e^{\prime }$ is a spanning tree of $G$.

Related

• Bipartite Graph