Breadth-First Search

Bipartite Graph

This is a more specific case of Graph Colouring with two colors.

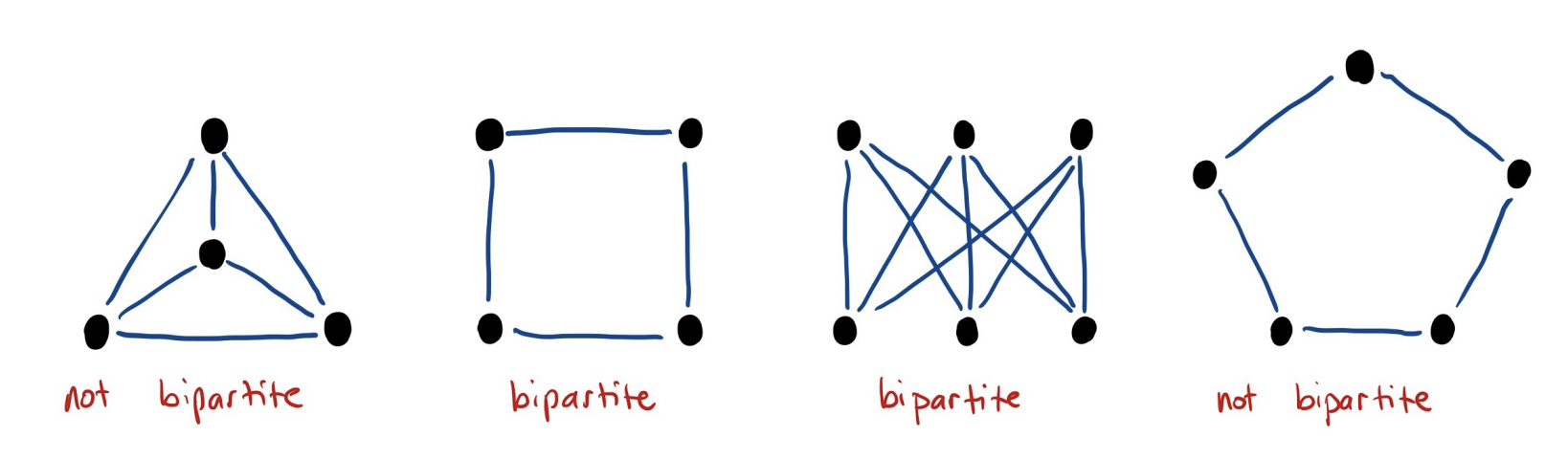
A graph is bipartite if and only if it is two-colorable.

Odd cycle

A graph is bipartite exactly when it does not contain a cycle with an odd number of edge

int n;
vector<vector<int>> adj; // Undirected Graph
 
vector<int> side(n, -1);
bool is_bipartite = true;
queue<int> q;
for (int st = 0; st < n; ++st) {
    if (side[st] == -1) {
        q.push(st);
        side[st] = 0;
        while (!q.empty()) {
            int v = q.front();
            q.pop();
            for (int u : adj[v]) {
                if (side[u] == -1) {
                    side[u] = side[v] ^ 1;
                    q.push(u);
                } else {
                    is_bipartite &= side[u] != side[v];
                }
            }
        }
    }
}
 
cout << (is_bipartite ? "YES" : "NO") << endl;

MATH239

Bipartite Graph

A graph is bipartite if its vertex set can be partitioned into two disjoint sets $A$, $B$ such that $V=A\cup B$ and every edge in $G$ has one endpoint in $A$ and one endpoint in $B$.

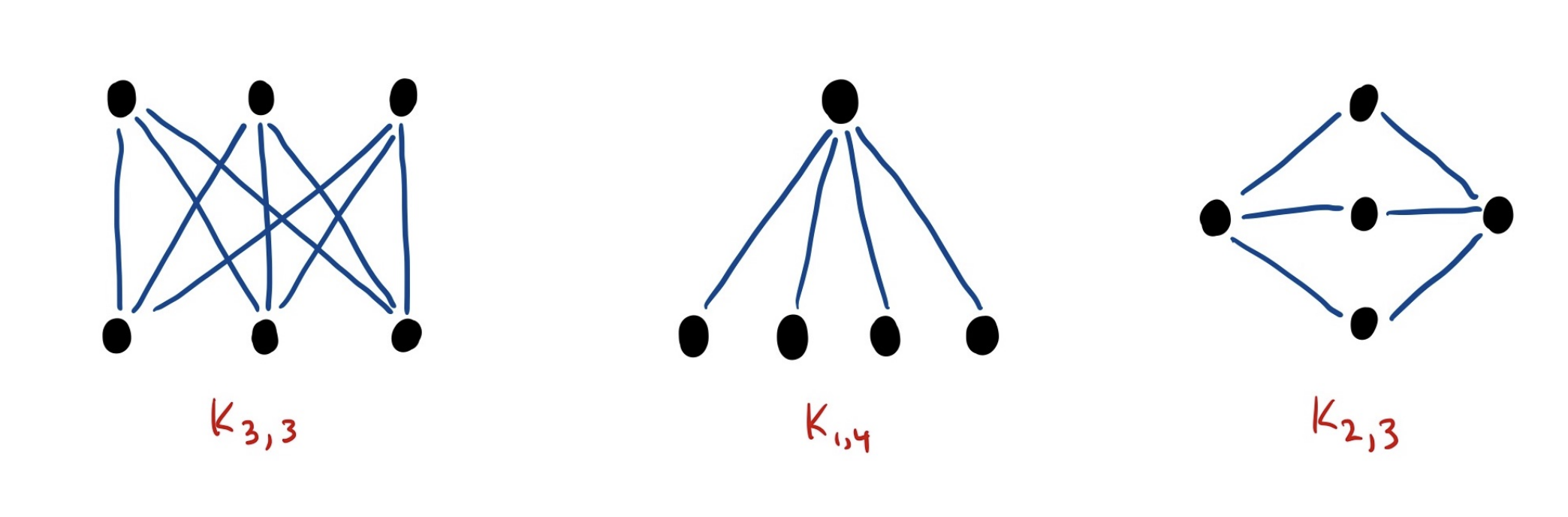
Complete Bipartite Graph

For positive integers $m$, $n$, the complete bipartite graph $K_{m,n}$ is the graph with bipartition $A$, $B$ where $|A|=m$ and $|B|=n$, containing all possible edges joining vertices in $A$ with vertices in $B$.

$\to$ Notice that there are $mn$ edges in $K_{m,n}$

Theorems

Theorem 5.3.2

A graph $G$ is bipartite $⟺$ it has no odd cycles.

How to Prove a Graph is Bipartite?

Create a bipartition, and show how the edges have one end in both sets.

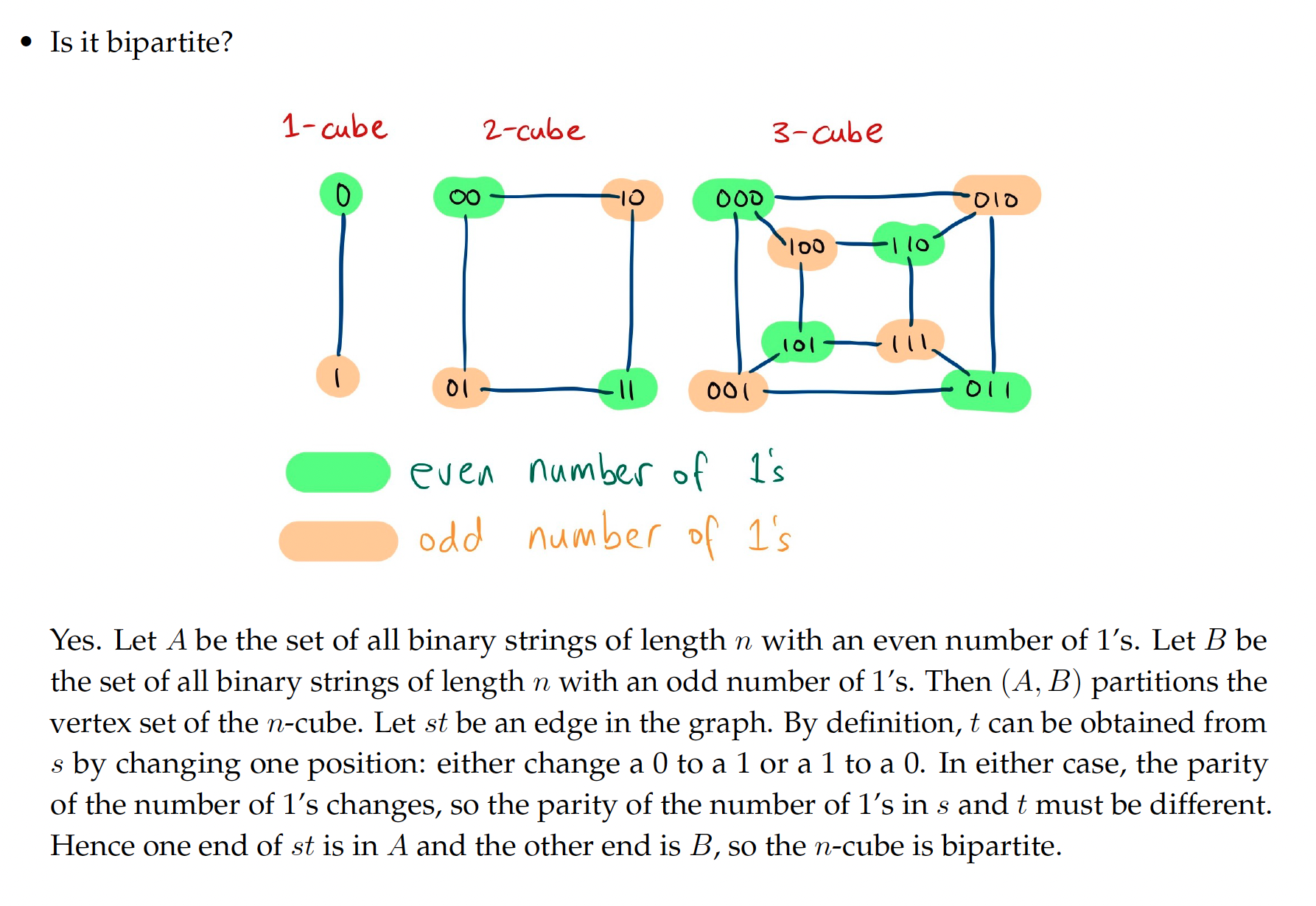
• Proof done using Connectedness:

Related

• n-cube graph

Problems

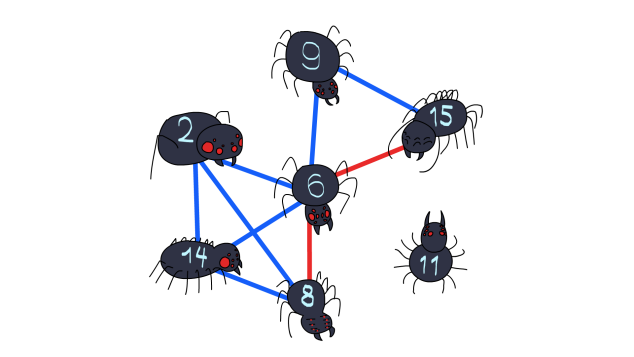
This friendly spiders codeforces problem 1775D can be solved with bipartite graphs!!