Strong Connectivity

A graph is strongly connected if there is a path from any node to all other nodes in the graph.

The strongly connected components of a graph divide the graph into strongly connected parts that are as large as possible. The strongly connected components form an acyclic component graph that represents the deep structure of the original graph.

You can solve 2-SAT using Kosaraju’s Algorithm.

From this blog

• A directed graph is called connected if, when you ignore direction, there is a path from every vertex to every other vertex.
• A graph is strongly connected if you still get paths everywhere when considering direction.

MATH239

Definitions

Connectness

A graph is connected if there exists a $u,v$-path for every pair of vertices $u,v$.

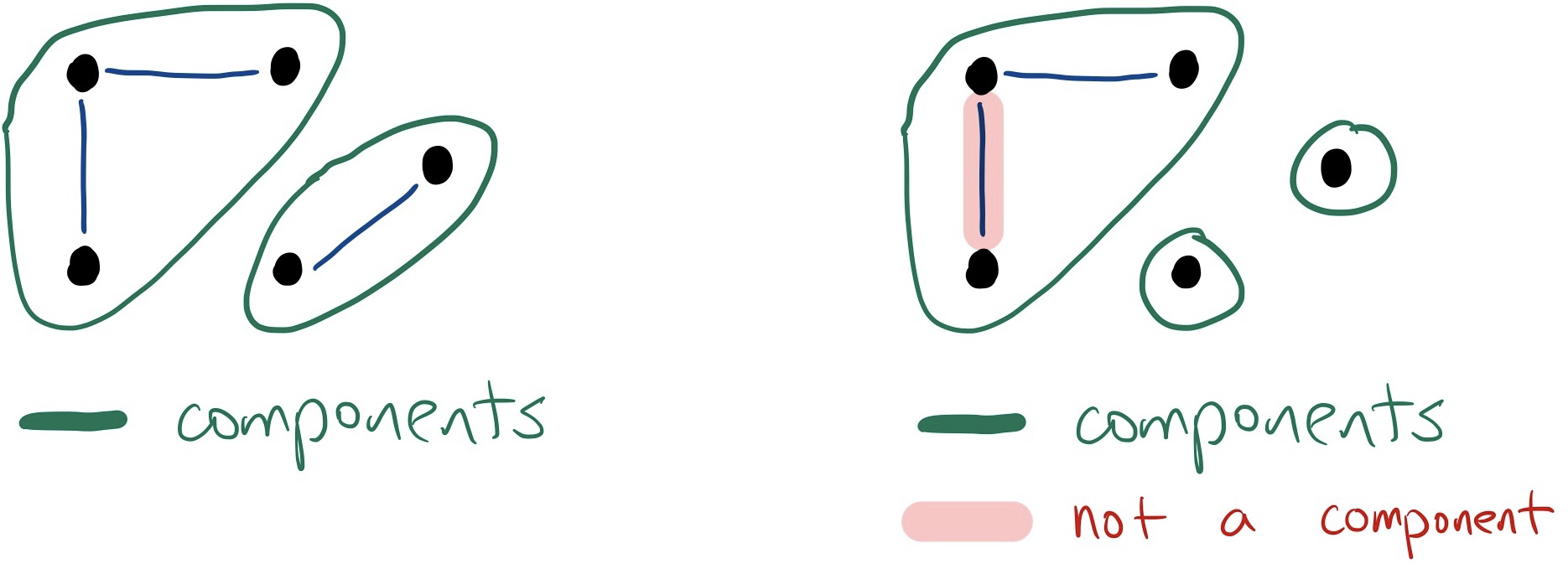
Component

A component $C$ of a graph $G$ is a connected subgraph of $G$ such that $C$ is not a proper subgraph of any other connected subgraph of $G$. (Equivalently, $C$ is a maximally connected subgraph of $G$.)

Graph Cut

Let $X\subseteq V(G)$. The cut induced by $X$ in $G$ is the set of all edges in $G$ with exactly one end in $X$.

Theorems and Lemmas

Theorem 4.8.2

Let $G$ be a graph and let $u\in V(G)$. A $u,v$-path exists for each $v\in V(G)$ if and only if $G$ is connected.

Theorem 4.8.5

A graph $G$ is disconnected if and only if there exists a non-empty proper subset of $X$ of $V(G)$ such that the cut induced by $X$ is empty.

• This illustrates the connection between Cuts and Connectedness

Theorem 4.9.2

Let $G$ be a connected graph. Then, $G$ has an Eulerian Circuit if and only if every vertex has even degree.

How to prove a graph is connected?

Use theorem 4.8.2 (from above): A $u,v$-path exists for each $v\in V(G)$ if and only if $G$ is connected.

• Set $u$ to a particular vertex in $G$. Then, prove that this vertex is connected to every other vertex $v$ through a particular $u-v$ path.

For example: