Baseline Fallacy
The base rate fallacy is a type of fallacy in which people tend to ignore the base rate (i.e., general prevalence) in favor of the individuating information (i.e., information pertaining only to a specific case).
Base rate neglect is a specific form of the more general Extension Neglect.
I think I had this kind of question from Intact, with the COVID-19 testing.
Example
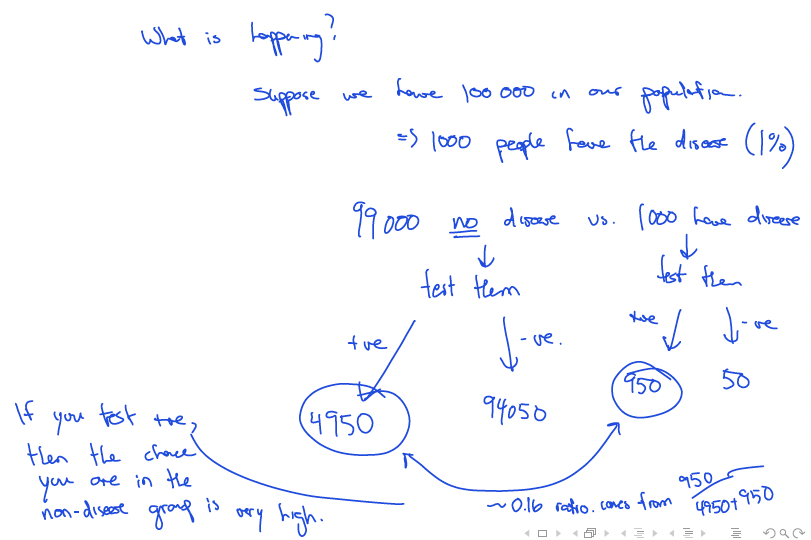
A person is getting tested for a disease that affects 1% of the population.
- A test is 95% accurate in true positivity. (Sensitivity)
- A test is 95% accurate in true negativity. (Specificity)
If a person tests positive, then what is the probability that they have the disease?
Note: These are not testing Precision.
Solution: = have the disease = don’t have the disease = test is positive = test is negative
We have the following probabilities:
This seems to tell us that the tests give really good results.
However, using Bayes’ Rule (?), we find that , which is really bad. This is due to Baseline Fallacy.
If you test positive, then the chance you are in the non-disease group is very high because the specificity is not high enough.
From PD20
Basically, being blinded by the larger picture.
Event-Specific Information: Dennis volunteers in the community, participates in a lot of extracurricular activities on campus, his grades are amazing, and don’t get him started on how qualified he feels he is for the job. He is going to get that job!
Base-Rate: 19 other students have applied to the same job.
Dennis’ unearned confidence that he will get the job arises from his fixation on his own situation. He is wrong to assume that his situation is all that matters in his assessment of whether he will get the job, and he is wrong to ignore the fact that he is competing against 19 others for the job. Yes, a good interview might sway the recruiters to choose him over the others, but Dennis’ chance of getting the job going into the interview is 1/20.