Distribution

Chi-Squared Distribution ${\chi }^2$

Very few real-world observations follow a chi-square distribution. The main purpose of chi-square distributions is Hypothesis Testing, not describing real-world distributions.

Definition 1:
Let $n$ be a positive integer. Then we say $W\sim {\chi }^2(n)$ if
$W=Z_1^2+Z_2^2+\cdots +Z_n^2$ where

• $Z_i\sim N(0,1)$, $Z_i$’s are independent
• $n$ a parameter that represents the Degrees of Freedom

Definition 2 using the PDF: $f(w)=\frac{1}{2^{\frac{n}{2}}\Gamma (\frac{n}{2})}{w}^{\frac{n}{2}-1}{e}^{\frac{-w}{2}},w\ge 0$ where

• $\Gamma (\alpha )$ is the Gamma Function

Expectation and Variance

• $E(X)=n=df$ where $df$ is the Degrees of Freedom
• $Var(X)=2n=2df$

If we apply CLT, we get that as $n\to \infty$, $W\sim N(n,2n)$

• $n=1⟹Z^2$
• $n=2⟹Exp$
• $\cdots ⟹{\chi }^2$ table
• $n=\infty ⟹Normal$

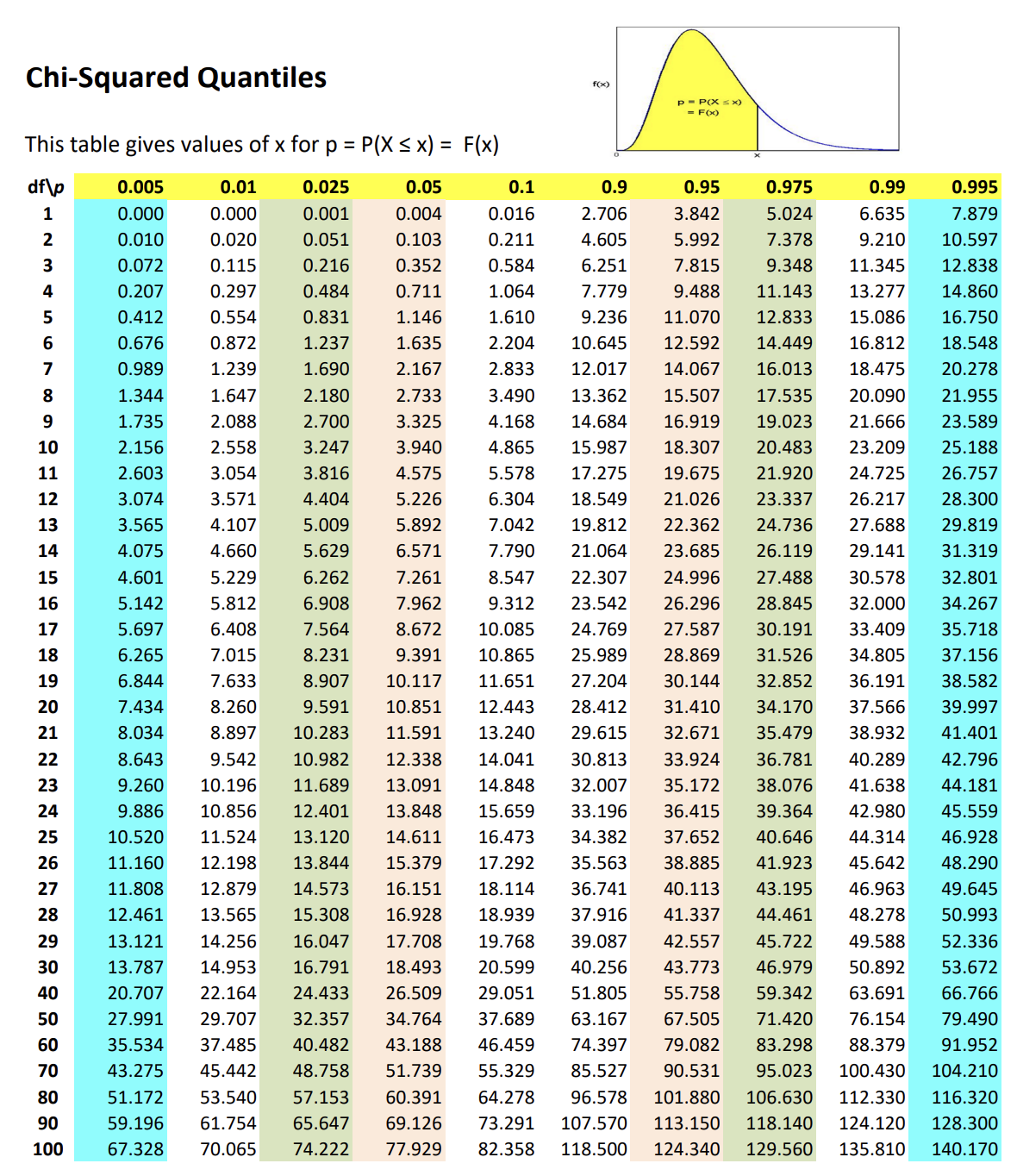
Chi-Squared Table

Examples

So in here, unlike in the Z-Table, you are given a degree of freedom and a probability, and this table gives you the $X$ value.

Since ${\chi }^2$ is one-tailed, then you just check the 95%,

Ex1: df =15, percentile = 0.9, you find that x = 22.307 Ex2: Let $W\sim {\chi }^2(11)$, Find $a$ and $b$ such that $P(a\le w\le b)=0.95$

You can consider the probabilities $0.025$ and $0.975$, so you have $P(3.816\le w\le 21.92)=0.95$.

Related

• Goodness of Fit
• Student’s t-Distribution