Central Limit Theorem

The Central Limit Theorem states that if you take sufficiently large random samples from the population with replacement (whose values are summed), then the distribution of the sample means will be approximately normally distributed.

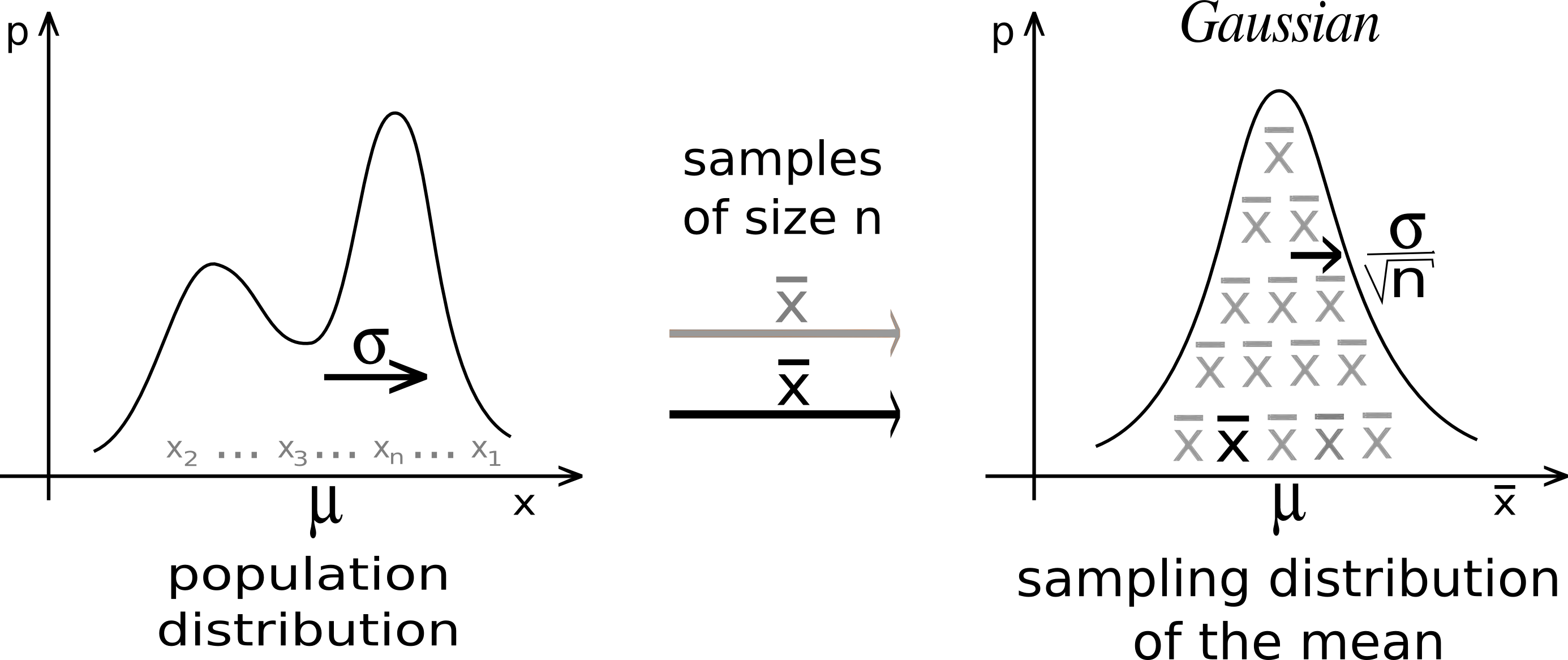
title: The Sampling Distribution of the Sample Mean (Theorem)
Let $X_1, X_2, \dots , X_n$ be i.i.d. $N(\mu, \sigma^2)$, then
$$S_n = \sum\limits X_i ∼ N(nμ, nσ^2)$$
$$X_n = \frac{1}{n}\sum\limits X_i ∼ N(\mu, \frac{σ^2}{n})$$

I know that this works, but I don’t know the theory on why it works. The teacher says the proof is done with Moment-Generating Functions.

title: CLT
The [[Law of Large Numbers]] tells us that the r.v. $\overline{X}_n$ approaches $\mu$ as $n$ approaches $\infty$. But how does $X_n$ behave?  
The Central Limit Theorem tells us that as $n → \infty$:  
$$X_n ∼ N \left(\mu, \frac{\sigma^{2}}{n}\right) \space OR \space Z = \frac{X_n - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0, 1)$$

This is so powerful because $X_n$ can model ANY distribution., For example, if $X\sim Bin(n,p)$ then $X\sim N(np,np(p-1))$ → wait is this CLT?

If $X_1,X_2,\dots ,X_n\sim Poi(\lambda )$, then $X_n\sim N(\lambda ,\frac{\lambda }{n})$

Proof

I asked for a proof in class for the CLT which the teacher gave, except I don’t understand it…

Let $X_1,X_2,\dots ,X_N$ be i.i.d r.v.s. with $E(X_i)=\mu$, $Var(X_i)={\sigma }^2$

Let $z=\frac{\overline{X}-\mu }{\frac{\sigma }{\sqrt{n}}}$, where $\overline{X}=\frac{1}{n}{\sum }_{i=1}^N{X}_i$ We will show that ${\lim }_{n\to \infty }{M}_z(t)=e^{\frac{t^2}{2}}$: Let $Y_i=\frac{X_i-\mu }{\sigma }$ $z=\frac{\overline{Y}-\mu }{\frac{\sigma }{\sqrt{n}}}$, $Y_i$ is i.i.d with $E(Y_i)=0$, $Var(Y_i)=1$

Then, we use the Moment-Generating Function $M_Z(t)=E[e^t]={\pi }_{i=1}^{n}E[e^{t\frac{y_i}{\sqrt{n}}}]=[M_{y_i}\frac{t}{\sqrt{n}}{]}^n$ Taking the limits, we have (2nd step to 3rd step jump is by Taylor Approximation, it seems by magic) ${\lim }_{n\to \infty }{M}_Z(t)={\lim }_{n\to \infty }[M_{y_i}(\frac{t}{\sqrt{n}}){]}^n={\lim }_{n\to \infty }[1+0+\frac{\frac{t^2}{2}}{n}{]}^n=e^{\frac{t^2}{2}}$

The central limit theorem is super interesting! Learned it while at Ericsson. Based around the Ericsson. Based around the Law of Large Numbers.

In my laymanns terms, take any distribution and randomly sample from it. Say if you sample at least 30 times, and you take the sum of those sampled values. Then repeat that process like 1000 times. If you plot the sums of those samples, it will follow a Normal Distribution.

The Continuity Correction

To convert discrete to continuous, we can apply a continuity correction to have a better approximation…? $P(X=4000)=P(3999.5<X<4000.5)$

To generate a Random Normal Number

Obtained from Xixian at Ericsson. I still don’t know enough to understand why this works.

Suppose $x_1$, $x_2$, and $x_N$ are independent samples chosen from the uniform distribution with the mean $\mu$ and variance ${\sigma }^2$. Let $y$ $y=\frac{({\sum }_{i=1}^N{x}_i-N\ast \mu )}{\sqrt{N}\ast \sqrt{\sigma })}$

Where

• $\sigma$ is the real Variance
• $\mu$ is the real mean of the distribution, NOT of the sample. (I made this fatal mistake in the implementation)

Then $y$ is a random variable with a standard normal distribution if $N$ is sufficient large, e.g, $N=30$ is usually the number used