Z-Score

The z-score represents number of Standard Deviations above or below that $X$ is from mean $\mu$.

If a Z-score is $0$, it indicates that our data point(s) $X$ is identical to the mean score. $Z=\frac{X-\mu }{\sigma }$

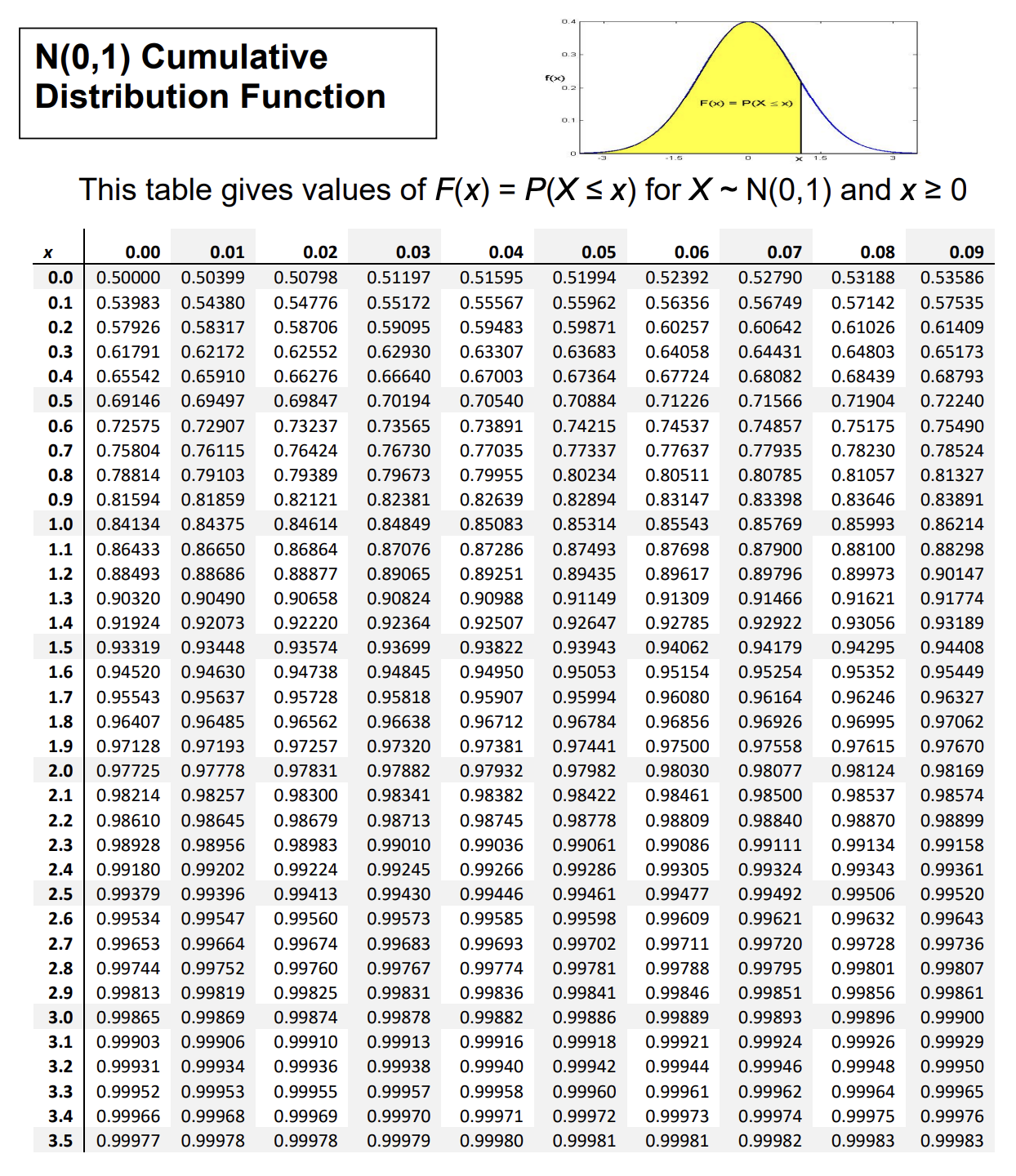
Z-Table

Mapping value to probability.

Ahh, so if you Z-score is 0, you see that the probability is exactly 50%, which makes sense, because the distribution is centered around $0$.

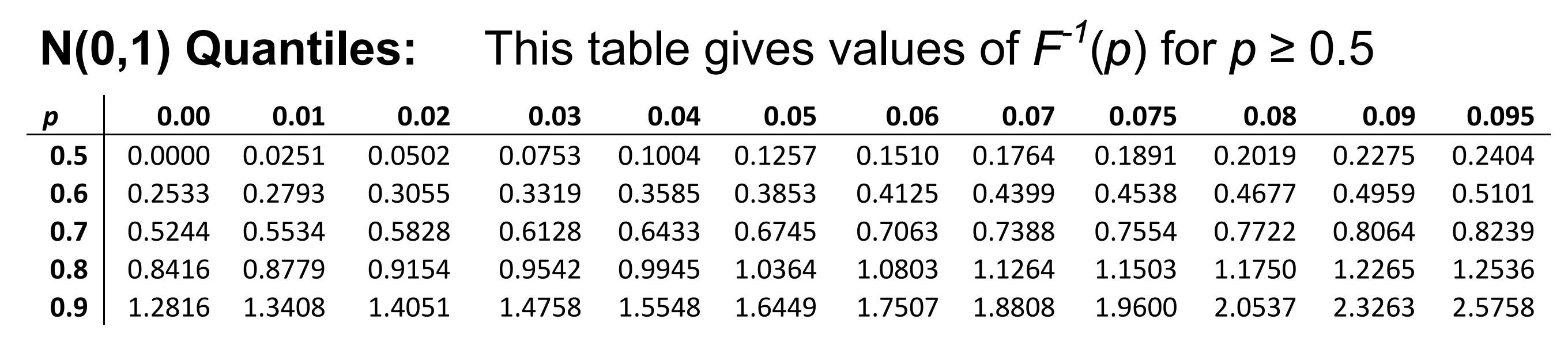
The Quantiles, this is just a reverse mapping of probability to original value.

Some Examples

It really helps if you draw the area under the distribution.

1. $P(Z\ge 1)=1-0.84134$
2. $P(Z\ge -1.2)=P(Z\le 1.2)=0.88493$
3. $P(Z\le -0.7)=1-P(Z\le 0.7)=1-0.75804$
4. $P(1\le Z\le 2)=P(Z\le 2)-P(Z\le 1)=0.97725-0.84134$