Statistics

Hypothesis Testing

I learned this in Enriched bio a while ago at Marianopolis College, I regret not learning this more seriously, as I have forgotten all of it now. Update: I am learning about it in STAT206!

Hypothesis is some claim (usually about a parameters) about the population.

Null Hypothesis ($H_0$): “Current belief”; conventional wisdom Alternate Hypothesis ($H_1/H_A$): Challenge to $H_0$

There are two types of test

• Two-tailed (what we stick to in STAT206, using $\ne$)
• One-tailed (using inequality $<$ or $>$)

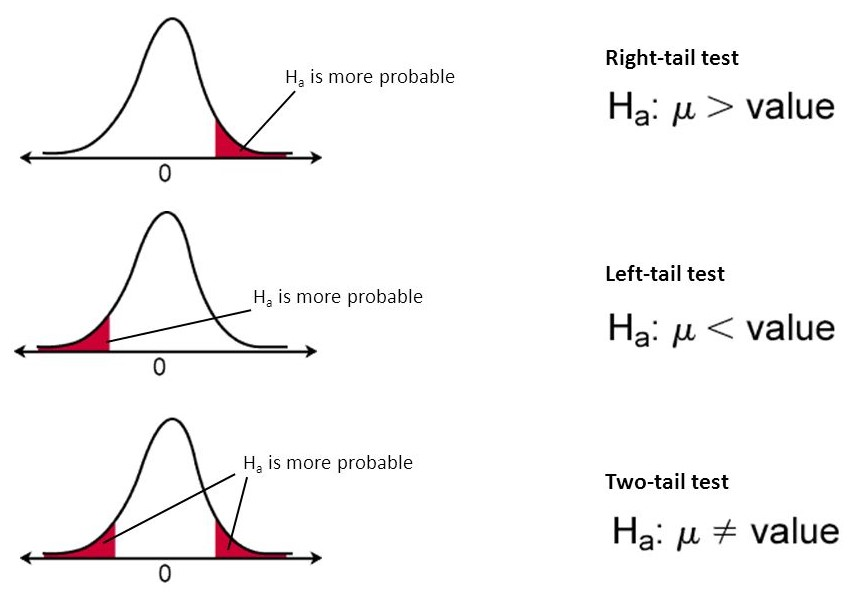
I finally understand this intuitively. If you fall within the region of rejection, then you reject your null hypothesis.

• We have enough evidence to support a claim that $H_1$ / $H_0$

You should form your hypothsis.

4-Step Method for Hypothesis Testing

1. Construct the Test Statistic
2. Calculate the value of the Test Statistic
   • Seems like we use the Pivotal Quantity for the appropriate distribution
3. Compute the p-value
   • This is a little hard and intimidating, I don’t know what values I should be looking at
   • Okay, I am starting to get it. I think you need to be careful about which test to use. If you
   • If you variance is known, use Z-Table.
   • If your variance is unknown, use the T-table, where your DOF is $n-1$.
   • There is also DOF of $n-2$ if you are doing linear regression??
4. Draw appropriate conclusions for the $p$-value
   • $p<0.05⟹$ reject $H_0$, fail to reject $H_1$
     • We can also say “we have enough evidence to support $H_1$”
   • $p\ge 0.05⟹$ fail to reject $H_0$, reject $H_1$
     • You can’t say the other way around, since 0.05 is not enough. You need to have another test
     • “There does not appear to be a difference between enough evidence to show that $H_1$”

Standard testing for a mean:

• There is not enough evidence to show a particular mean?? But that is kind of iffy

Comparing two means:

• Support of $H_1$: There is not enough evidence to show that the means are the same
• Support of $H_0$: There is not enough evidence to show that the means are different

Linear

• There seems to be linear relationships between X and Y.
• There is not enough evidence to show that a linear relationship exists between X and Y.

Normal Hypothesis Testing

Let’s illustrate the 4-step method through an example of normal hypothesis testing.

Suppose $Y_1,\dots Y_{25}\sim N(\mu ,144)$, $Y_i$s are independent. $n=25$ and $\overline{y}=50$. We want to test the following hypothesis:

• $H_0:\mu =45$
• $H_1:\mu \ne 45$

Can we conclude that our sample data supports $H_1$?

Step 1: Construct the Test Statistic

See Test Statistic for more information. We’ve seen this before in Test Statistic for more information. We’ve seen this before in Confidence Interval: $\overline{Y}\sim N\left(\mu ,\frac{{\sigma }^2}{n}\right)⟹\frac{\overline{Y}-\mu }{\frac{\sigma }{\sqrt{n}}}=Z\sim N(0,1)$ You conclude that you have the following $D$ value: $D=|Z|$

Step 2: Calculate the Test Statistic

$d=\frac{\overline{y}-45}{\frac{12}{5}}=\frac{50-45}{\frac{12}{5}}\approx 2.1$

Step 3: Compute the p-value

• If you variance is known, use Z-Table.
• If your variance is unknown, use the T-table, where your DOF is $n-1$.

P(Z \leq 2.1) &=0.98214\\ [3pt] \implies P(|Z| \geq 2.1)&=2(1-0.98214)\\ [3pt] \text{p-value}&=0.03572 \end{aligned}$$ This is a little confusing, it's in the similar lens of the idea I talked about in [[notes/Confidence Interval|Confidence Interval]] when retrieving the right Z-value. ![[attachments/Screen Shot 2022-12-14 at 11.07.03 PM.png]] ##### Step 4: State your conclusion Since $p < 0.05$, we have strong strong evidence against $H_0$. Therefore, we reject $H_0$, and fail to reject $H_1$. If you want to test for unknown $\sigma$, you use the same idea as you saw in [[notes/Confidence Interval|Confidence Interval]], notes is page 347. You use the [[notes/Student's t-Distribution|t-table]]. ### Binomial Hypothesis Testing Ex: A survey of 1000 Americans asked who they would vote for; Biden (52%) or Trump (48%). Is this election too close to call? $H_0: \theta = \frac{1}{2}$ $H_1: \theta \neq \frac{1}{2}$ $$H \ Y = \# \ \text{of people voting for Biden} \implies Y \sim Bin(1000, \theta)$$ Step 1: Construct the Test Statistic We use the [[notes/Pivotal Quantity|Pivotal Quantity]] for the binomial [[notes/Confidence Interval|Pivotal Quantity]] for the binomial [[notes/Confidence Interval|Confidence Interval]]. $$\frac{Y - n\theta}{n\theta \sqrt{(1-\theta)}}= Z \sim N(0,1)$$ $$\implies Z = \frac{Y - 1000 \cdot \frac{1}{2}}{\sqrt{1000 \cdot \frac{1}{2}\cdot \frac{1}{2}}}$$ $$\implies D = \left| \frac{Y-500}{\sqrt{250}} \right |$$ Step 2: Calculate the [[notes/Test Statistic|Test Statistic]] $$d = \left| \frac{520-500}{\sqrt{250}}\right| \approx 1.26$$ ### Relationship with [[notes/Confidence Interval|Confidence Interval]] So they are the same idea? 1. A 95% [[notes/Confidence Interval|Confidence Interval]] 2. Conducting a [[notes/Hypothesis Testing|Hypothesis Test]] using a 0.05 cutoff for the [[notes/p-value|p-value]] - $H_0: \theta = \theta_0$ - $H_1: \theta \neq \theta_0$ - For the CI, we find $\theta_0 \pm a$ - For hypothesis test, if $\theta$ is in $\theta_0 \pm a$, then we conclude $H_0$. Else, we conclude $H_1$. ### Hypothesis Testing with Two Means This is where I am getting confused. ### Related - [[notes/Test Statistic|Test Statistic]] - [[notes/Type I and Type II Error|Type I and Type II Error]] - [[notes/Chi-Squared Distribution|Chi-Squared Distribution]] - Chi-Square Goodness of fit test - [[notes/p-value|p-value]] - [[notes/Z-Score|Z-Score]]