Floating-Point Number System

Float number.

https://codingnest.com/the-little-things-comparing-floating-point-numbers/

First introduced through PMPP. Formally learned through CS370.

Representing a Real Number

Each positive number in $\mathbb{R}$ can be represented in normalized form by $0.d_1{d}_2\cdots d_t\times {\beta }^p$

where

• $d_k$ are digits in base $\beta$, that is, $0,1,\dots ,\beta -1$;
• ‘normalized’ means $d_1\ne 0$;
• exponent $p$ is an integer (positive, negative or zero).

The sequence of digits $0.d_1{d}_2{d}_3\cdots \times {\beta }^p$ is called the mantissa (also significand).

Knowing this, we can define a Floating-Point Number System.

Floating Point Number System

Every floating point number system $F$ that we will consider can be characterized by four integer parameters, $\{\beta ,t,L,U\}$. $F=\{\beta ,t,L,U\}$

• $\beta$ is the base (ex: 10)
• $t$ is the number of digits in the mantissa (represents density / precision)
• $L$ and $U$ are bounds on the exponent $p$ (represents extent / range)

Thus, the numbers in such a system are precisely those of the form $\pm 0.d_1{d}_2...d_t\times {\beta }^p\text{for}L\le p\le U\text{ and }{d}_1\ne 0$ or $0$ (a very special floating point number)

In practice, there are 2 common standardized floating point systems:

1. IEEE Single Precision (fp32)
2. IEEE Double Precision (fp64)

See IEEE Floating Point Standard.

IEEE single precision: $\{\beta =2;t=24;L=-126;U=127\}$ IEEE double precision: $\{\beta =2;t=53;L=-1022;U=1023\}$

There’s also FP16 (half-precision)

This is super confusing

Go see the IEEE Standard because they split numbers differently than how we see it at the beginning of this note. IEEE uses a normalization convention in which the first non-zero digit lies to the left of the decimal point, rather than the right.

Int vs Floats and Doubles

I was thinking like of an Integer, where the largest signed int is $2^{31}-1$. But it’s actually more complicated for floats and doubles.

See IEEE Floating Point Standard for the 3 parts of the number (sign, exponent, mantissa)

Properties of Floating Point Numbers

Relationship between Real and Floating Point Numbers

This is really important to understand.

Generally case, $fl(x)\ne x$ because most real numbers cannot be represented exactly. In order to compute $fl(x)$, we must modify $x$ to become a valid representable floating point number, typically by eliminating some of its smaller digits.

One way to think about going from real to floating number is laying it out in slots.

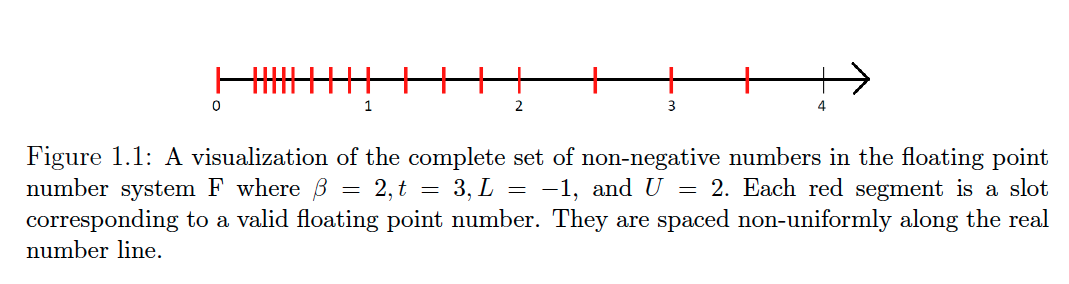
Important

Floating Point Numbers are not uniformly spaced. This is due to the way they are designed (see the equation at the beginning of the page).

Numbers that are closer to zero, which have more negative exponents, are spaced more closely together. Conversely, numbers with larger magnitudes, characterized by more positive exponents, are spaced further apart. See Fixed-Point Number System for fixed spacing.

You can see how the spacing is

$0.d_1{d}_2{d}_3\cdots \times {\beta }^p$

The conversion from real to floating number is called round-off error.

See Machine Epsilon.