Graph Theory

Learned formally in MATH239. See Graph for implementation for a programming perspective.

Relationship with Combinatorics

I learned graph theory in my combinatorics course, and although it seems like they are completely different, I think it’s because graphs also involve counting: number of paths between nodes, number of subgraphs, ways to color a graph, etc.

Concepts

Graph Density

The average degree of a vertex in $G$ is $\frac{2|E(G)|}{|V(G)|}$ This is a measure of the density of a graph.

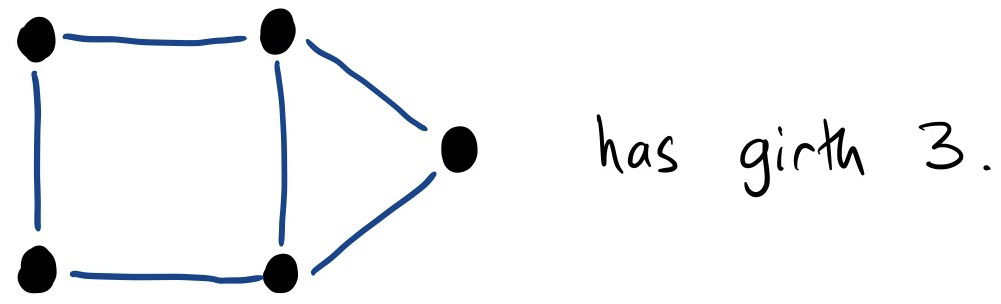
Girth

The girth of a graph is the length of its shortest cycle. If $G$ has no cycle, then its girth is $\infty$.

Subgraph

A graph $H$ is a subgraph of a graph $G$ if the vertex set of $H$ is a (non-empty) subset of the vertex set of $G$ ($V(H)\subseteq V(G)$) and the edge of $H$ is a subset of the edge set of $G$ ($E(H)\subseteq E(G)$) where both endpoints of any edge in $E(H)$ are in $V(H)$.

• If $V(H)=V(G)$, we call $H$ a spanning subgraph
• If $H\ne G$, then $H$ is a proper subgraph

Walk

A $u,v$-walk is a sequence of alternating vertices and edges $v_0,v_0{v}_1,v_1,v_1{v}_2,v_2,...,v_{k-1},v_{k-1}{v}_k,v_k$ where $u=v_0$ and $v=v_k$. This walk has length $k$.

• a walk is closed if $v_0=v_k$

Path (also called simple path)

A $u,v$-path is a $u,v$-walk with no repeated vertices.

• Note that since no vertices are repeated, no edges are repeated either

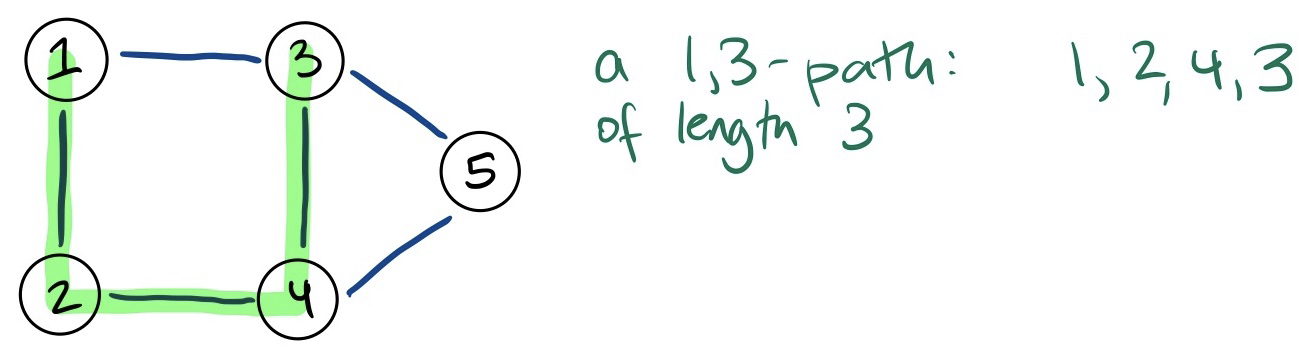
Theorem 4.6.2

If there is a $u,v$-walk in $G$, then there is a $u,v$-path in $G$.

Corollary 4.6.3

If there is a $u,v$-path and a $v,w$-path in $G$, then there is a $u,w$-path in $G$.

Cycle

A cycle of length $n$ is a subgraph with $n$ distinct vertices $v_0,v_1,...,v_{n-1}$ and $n$ distinct edges $v_0{v}_1,v_1{v}_2,...,v_{n-2}{v}_{n-1},v_{n-1}{v}_0$.

• In a simple graph, the minimum length of a cycle is 3 (the triangle)

Theorem 4.6.4

If every vertex in $G$ has degree at least 2, then $G$ contains a cycle.

Bridge

An edge $e$ of $G$ is a bridge (or cut-edge) if $G-e$ has more components than $G$.

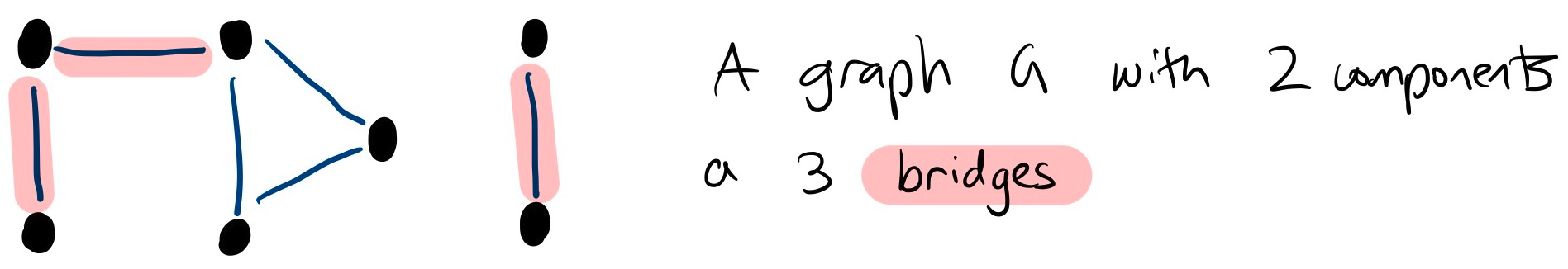
Lemma 4.10.2

If $e=xy$ is a bridge in a connected graph $G$, then $G-e$ has exactly 2 components, and $x$ and $y$ are in different components of $G-e$.

Theorem 4.10.3

An edge $e$ is a bridge of $G$ if and only if it is not contained in any cycle of $G$.

This fully characterizes bridges:

• edge in cycle $⟺$ edge is not a bridge
• edge not in cycle $⟺$ edge is a bridge

Types of Graphs

• Planar Graph
• Petersen Graph
• k-Regular Graph
• Complete Graph
• Bipartite Graph
• Interference Graph
• Connected Graph

Visualization

• https://csacademy.com/app/graph_editor/

Related

• Graph Cover
• Tree