Feature Point

Keypoint

Notes taken from Cyrill Stachniss.

Resources

• Visual Feature Part 1: Computing Keypoints (Cyrill Stachniss)
  • Slides here

Corner = two edges in roughly orthogonal directions Edge = a sudden brightness change

Corners are great because they are very localizable in varying lighting conditions. This is why people focus on corners to get keypoints.

Finding Corners

To find corners we need to search for intensity changes in two directions.

Compute the SSD of neighbour pixels around $(x,y)$ $f(x,y)={\sum }_{(u,v)\in W_{xy}}(I(u,v)-I(u+\delta u,v+\delta v){)}^2$

• $I(u,v)$ is the actual intensity value of the pixel at position $(u,v)$
• $\delta u$ and $\delta v$ are simply small displacement values, they are NOT partial derivatives
• $W_{xy}$ is a local patch around $(x,y)$

Using Taylor expansion, we obtain that $I(u+\delta u,v+\delta v)$ is approximately $I(u+\delta u,v+\delta v)\approx I(u,v)+\left[\begin{array}{cc}{J}_x& J_y\end{array}\right]\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]$ Plugging back into $f(x,y)$, we see that the taylor approximation leads to $f(x,y)\approx {\sum }_{(u,v)\in W_{xy}}{\left(\left[\begin{array}{cc}{J}_x& J_y\end{array}\right]\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]\right)}^2$ Written in a matrix form as $f(x,y)\approx {\sum }_{(u,v)\in W_{xy}}{\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]}^T\left[\begin{array}{cc}{J}_x^2& J_x{J}_y\\ J_x{J}_y& J_y^2\end{array}\right]\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]$

• the derivation for this comes from expanding $(J_x\delta u+J_y\delta v{)}^2=J_x^2\delta u^2+2J_x{J}_y\delta u\delta v+J_y^2\delta v^2$

We can move the sums inside the matrix to get the Structure Matrix! $f(x,y)\approx {\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]}^T\left[\begin{array}{cc}{\sum }_{\text{W}}{J}_x^2& {\sum }_{\text{W}}{J}_x{J}_y\\ {\sum }_{\text{W}}{J}_y{J}_x& {\sum }_{\text{W}}{J}_y^2\end{array}\right]\left[\begin{array}{c}\delta u\\ \delta v\end{array}\right]$

J_x J_y has become J_y J_x for one of the terms?

This is more for convenience. $J_x$ and $J_y$ are merely real numbers.

Eigenvalue and Jacobian Matrix?

Cyrill talks about Eigenvalues at 19:30 when referencing the structure matrix. What do eigenvalues have to do with the eigenvalue?? I think of it as just a large value signifies a large change, high gradient.

Also, how are we going to deal with different orientations?

“We want to find a matrix with 2 large eigenvalues”. That makes it a good corner.

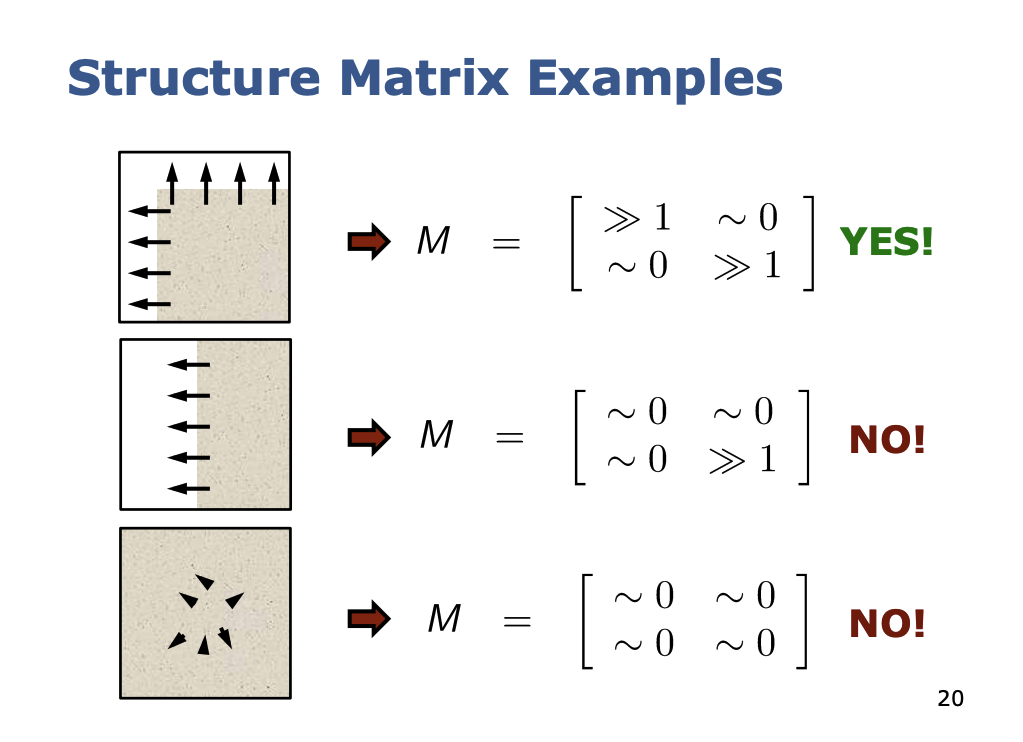
He thens introduces 3 similar approaches that were introduced in the 1990s for feature detection:

• Harris Corner
• Shi-Tomasi Corner Detector
• Forstner Operator

All of them rely on the Structure Matrix, but they use a different criterion to decide if a point is corner or not.

I don't really understand the eigenvalue part of this....

I guess I don’t really understand how eigenvalues work, so it is important to review that.

Consider points as corners if their structure matrix has two large eigenvenlues values.

Implementation Remarks

• RGB to gray-scale conversion first
• Real images are affected by noise, smoothing of the input is suggested

This is a great summary diagram, to see high level how things work

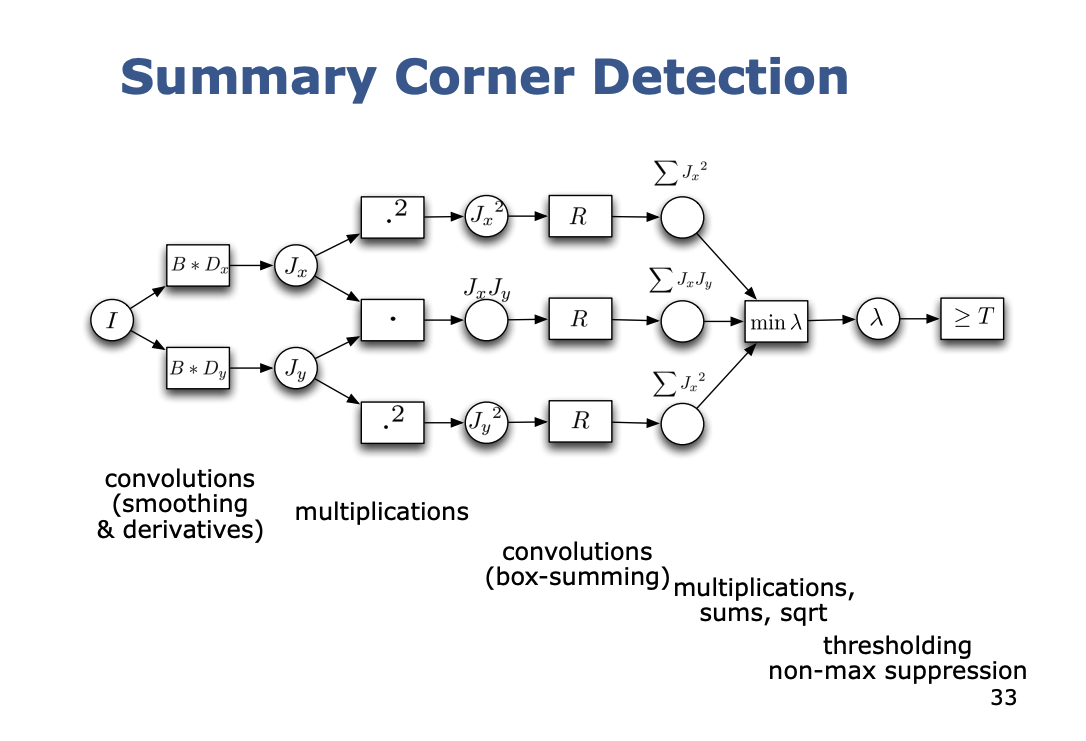
• $B$ is the smoothing operator
• $D_x$ is generally a Sobel Operator

Part 2: Difference of Gaussians

Used for SIFT descriptors

In Summary

The 2 approaches are key ingredients of most hand-designed features

1. Structure Matrix
2. Difference of Gaussians

Nowadays, features completely learned from data.