Softmax Function
Softmax is used to convert a set of values to a normalized probability distribution. It also amplifies differences between values (explained below).
is called the “logit”.
In code, we have simply:
def softmax(X):
exps = np.exp(X)
return exps / np.sum(exps)We use the Softmax Function to compute the Cross-Entropy Loss.
Resources
Why don't we just divide by the sum?
Simply dividing each score by the sum of all scores converts scores to probabilities. However, it doesn’t handle negative values well and lacks the ability to amplify differences between scores.
Ex: x = [-0.3, 0.3]. The sum is 0 so -0.3/0 is undefined and would not work.
Amplifying differences: illustrated
What do you mean by amplifying the differences?
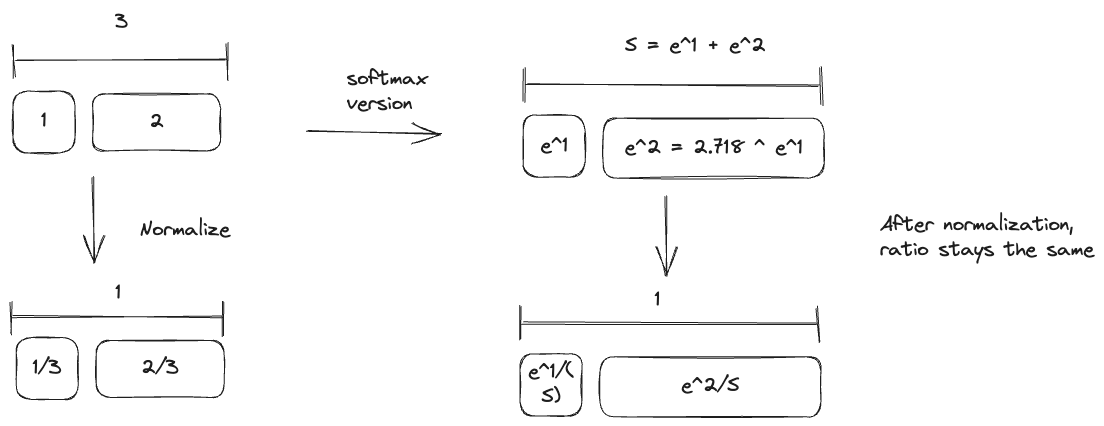
Consider if your input is 1 and 2. By passing it through an exponential function, you amplify the difference.
But you are normalizing afterwards, so it shouldn't matter?
When you normalize, you are only reducing down the numbers, but the ratio remains the same.
- Multinomial Logistic Regression
- probability distribution
The loss of 0 is the theoretical minimum, but the correct class should go towards infinity, and incorrect classes should go towards negative infinity.
logits = torch.tensor([100.0, 0.0, 0.0, 0.0])
torch.softmax(logits, dim=0)
# tensor([0.9584, 0.0176, 0.0065, 0.0176])Numeric Stability Problems
https://stackoverflow.com/posts/49212689/timeline
Softmax function is prone to two issues:
- Overflow: It occurs when very large numbers are approximated as
infinity - Underflow: It occurs when very small numbers (near zero in the number line) are approximated (i.e. rounded to) as
zero
To combat these issues when doing softmax computation, a common trick is to shift the input vector by subtracting the maximum element in it from all elements. For the input vector x, define z such that:
def stable_softmax(x): # Assumes x is a vector
z = x - max(x)
exps = np.exp(z)
return exps/np.sum(exps)Softmax Temperature
Learned from this 3b1b video https://www.youtube.com/watch?v=wjZofJX0v4M.
- Essentially tunes the aggressiveness of the softmax function
- Low temperature (i.e. T = 0) will make it select only the largest value
- Higher temperature will more uniformly spread out the values
Instead of , you use , where is the temperature.
This blog is useful: