Distribution

Normal Distribution

The MOST powerful distribution. Normal distribution is a probability distribution that is symmetric about the mean $\mu$, where data near the mean occur more frequently.

Normal Distribution (Definition)

We say that a r.v. $X$ is normally distributed, $X\sim N(\mu ,{\sigma }^2)$, if its p.d.f., $f$, is

$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}$ where

• $\mu$ is the mean or expectation of the distribution (and also its median and mode),
• $\sigma$ is its Standard Deviation

Normal Distribution is symmetrical around $\mu$, i.e. $f(x+\mu )=f(x-\mu )$ where $\mu$ is the mean, mode, and median.

Expectation and Variance

• $E(x)={\int }_{-\infty }^{\infty }xf(x)dx=\mu$ (the calculation for this is pretty messy)
• $Var(X)={\sigma }^2$

Standard Normal Distribution (Definition)

The standard Normal Distribution has $\mu =0$ and $Var(X)=1$, i.e. $Z\sim N(0,1)$. We have the p.d.f. $\varphi$ $\varphi (z)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{z^2}{2}}$

I learned the matrix form from the SLAM book.

Multi-dimensional Normal Distribution (Matrix-Form Definition)

The probability density function $f$ is

$f(x)=\frac{1}{\sqrt{(2\pi {)}^{N}det(\Sigma )}}exp\left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)$

Also see Gaussian Variable.

Where do we see gaussians in the real world?

• Height Distribution: Human heights follow a Gaussian distribution.
• IQ Scores: IQ scores typically follow a Gaussian distribution.
• Measurement Errors: Instrument measurement errors often have a Gaussian distribution.
• Stock Returns: Daily stock returns frequently exhibit a Gaussian distribution.

Z-table (Standard Normal z-table)

The z-table table gives values of the CDF $F(x)=P(X\le x)$ for $X\sim N(0,1)$ and $x\ge 0$.

What is really cool is that we can go from the standard normal distribution to another normal distribution with a particular mean and variance, using the theorem below:

Theorem

If $X\sim N(\mu ,{\sigma }^2)$ and $Z=\frac{X-\mu }{\sigma }$, then $Z\sim N(0,1)$

Look at the page on Z-Score

Example Exercise

Example: Suppose that final grades in this course follow a normal
distribution with $\mu =75$ and ${\sigma }^2=64$.

1. Find the probability that a student has a final grade of 83 or more.

2. Calculate the 95th percentile.

3. We have that $X\sim N(75,64)$, so find $P(X\ge 83)$ $Z=\frac{x-\mu }{\sigma }=\frac{83-75}{8}\le 1.6449$ $P(Z\le 1.6449)=0.94950$

4. We solve this by using the $N(0,1)$ Quantile table. $P(Z\le z)=0.95⟹P(Z\le 1.6449)=0.95$ $Z=\frac{x-\mu }{\sigma }=\frac{x-75}{8}\le 1.6449$ Therefore, we conclude that $X\le 75+8\cdot 1.6449$

Part 2: A sample of 9 students is taken. Find

1. $P(S\ge 700)$
2. $P(\overline{X}<73)$

I’m not sure if I understand correctly, but there is this Variance of the mean value that I need to use, instead of the direct variance.

$S\sim N(75\cdot 9,9\cdot 64)$ $P(S\ge 700)=P(Z_s\le 1.04)=1-0.85083$

2. $\overline{X}\sim N(75,64/9)$ $P\left(Z<\frac{-3}{4}\right)=1-0.77337$ (I don’t know if $Z<\frac{-3}{4}$ is correct, might be a typo)

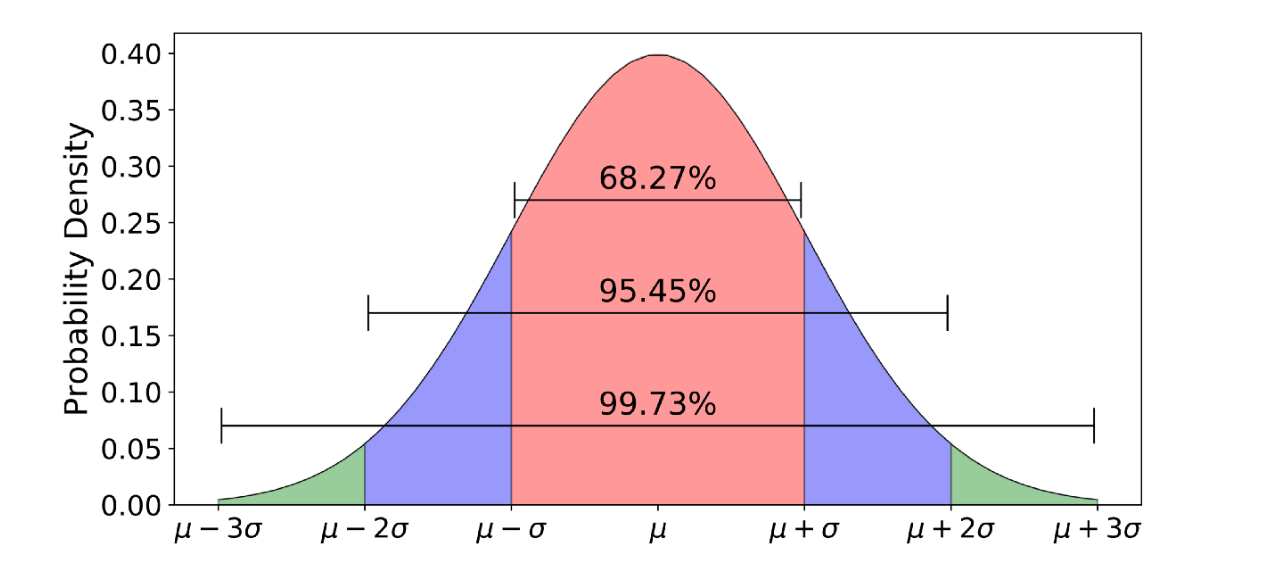
The 68-95-99 rule

The 68-95-99 rule is based on the mean and standard deviation. It says:

• 68% of the population is within 1 standard deviation of the mean.
• 95% of the population is within 2 standard deviation of the mean.
• 99.7% of the population is within 3 standard deviation of the mean.

Generating Normal Distributions in Code

To randomly sample from the Normal Distribution, we have a few options (Learned from Ericsson):

• Box-Muller Transform
• Marsaglia Polar Method
• Ziggurat Algorithm
• Central Limit Theorem

Related

• Gaussian Variable