Random Variable

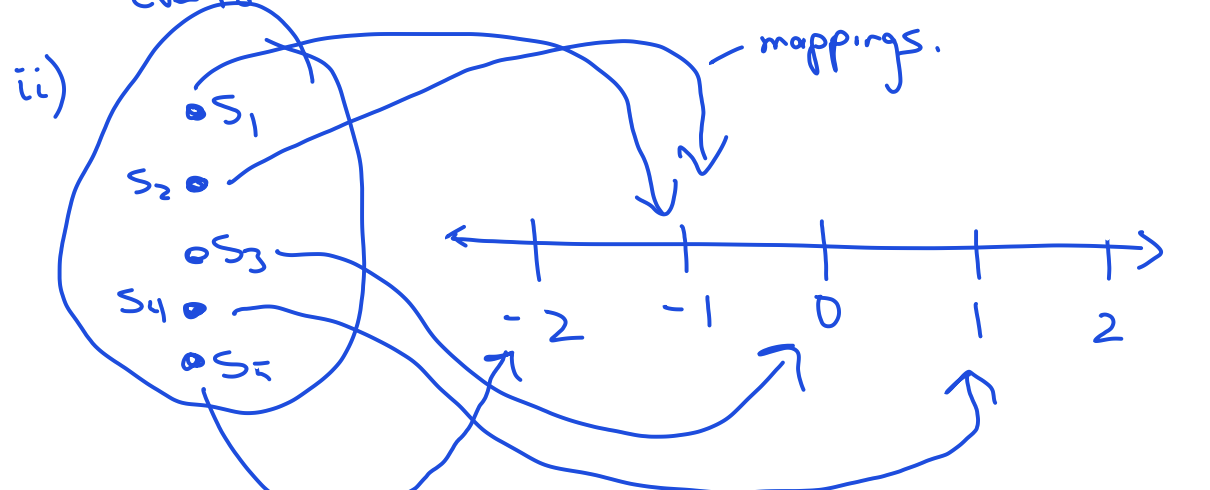
$X$ is a random variable (r.v.) if it is a function that maps each outcome of a random experiment (sample space $S$) to an element in $\mathbb{R}$. $X:S\to \mathbb{R}$

Ex: You roll a dice twice. We define $X$ as the sum of the faces, so it maps $(2,3)$ to $5$

• Domain: Set of outcomes in in the experiment $(x_1,x_2,\dots ,x_n)$
• Range: Real value

The random variable can follow various Distributions (see this page for more), such as

• Bernoulli Distribution
• Binomial Distribution
• etc.

There are two types of random variables:

1. Discrete Random Variable: Takes on Integer values
   • Uses Probability Mass Function
2. Continuous Random Variable: Takes on real values. Ex: Measuring heights of people
   • Uses Probability Density Function

Other Notes

1. The experiment is random, the function, $X$, is not.
   • This is confusing. The function is deterministic, input is random, but output behaviour is known. It would be stupid if the function is not deterministic.
   • Ex: Roll a die 3 times. Define $X=|\text{ \# heads - \# tails }|$
     • In this case, the actual coin flip (input) is random. However, calculating the function to determine $X$ is not, we know how to compute it and it is the same every time based on the input.
2. Geometric Interpretation of an r.v.
   1. 

title: [[Independence (Statistics)]] of [[Random Variable]]s
Random variables $X$ and $Y$ are independent if: 
$$P(X = x, Y = y) = P(X = x) \cdot P(Y = y), \forall x, y$$

title: Relationship with [[Binomial Distribution]]
If $X ∼ Bin(n, p)$, $Y ∼ Bin(n, p)$, and $X$ and $Y$ are independent, then $X + Y ∼ Bin(n_1 + n_2, p)$

Concepts

• Probability Mass Function
• Cumulative Distribution Function