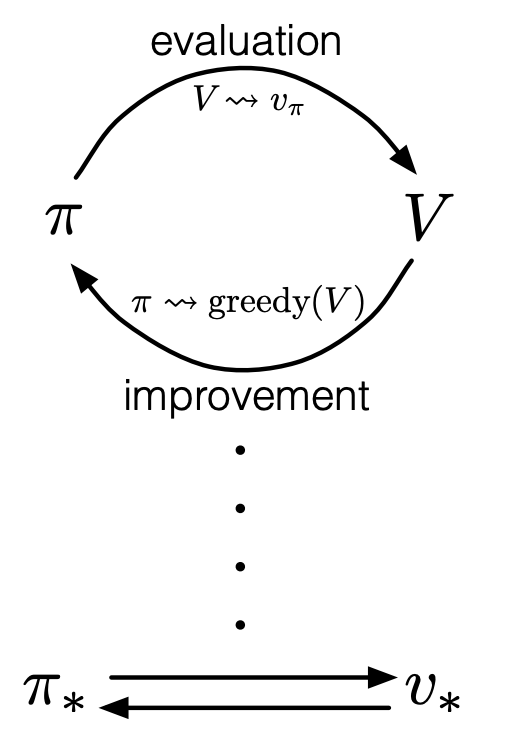
Generalized Policy Iteration

This is KEY to understanding how reinforcement learning works.

Generalized Policy Iteration refers to the general idea of letting policy-evaluation and policy-improvement processes interact.

• Computing Value Function with Value Function with Dynamic Programming in Reinforcement Learning
• Monte-Carlo Control
• TD Control

Steps

• Initialize policy $\pi$
• Repeat
  • Policy evaluation: Compute $Q_{\pi }$ for model-free, $V_{\pi }$ for model-based
  • Policy improvement: update $\pi$ ${\pi }^{\prime }(s)=\underset{a}{\mathrm{argmax}}{Q}_{\pi }(s,a)$

Key Terminologies

Prediction / Learning → policy evaluation Control → policy-improvement

Some Ideas that I need to master

In David Silver’s diagrams, the up direction is to find $v_{\pi }$, while the down arrows are to find $\pi$.

With Model-Based problems, we use our full knowledge of the Markov Decision Process, using DP combined with Value Iteration or Value Iteration or Policy Iteration..? For the policy improvement, we use a policy that acts greedily with respect to V(s).

However, in Model-Free, where we don’t know the environment, we don’t have that luxury. Greedy policy improvement over V(s) requires model of MDP.

In model-free, we use $Q(s,a)$. We reduce the burden. We can cache?

David Silver teaches two main methods: Monte-Carlo (full backup) and TD (bootstrap).