Unsupervised Learning Clustering Method
K-Means Clustering
This is a simple representation learning algorithm, which groups similar data points together in clusters.
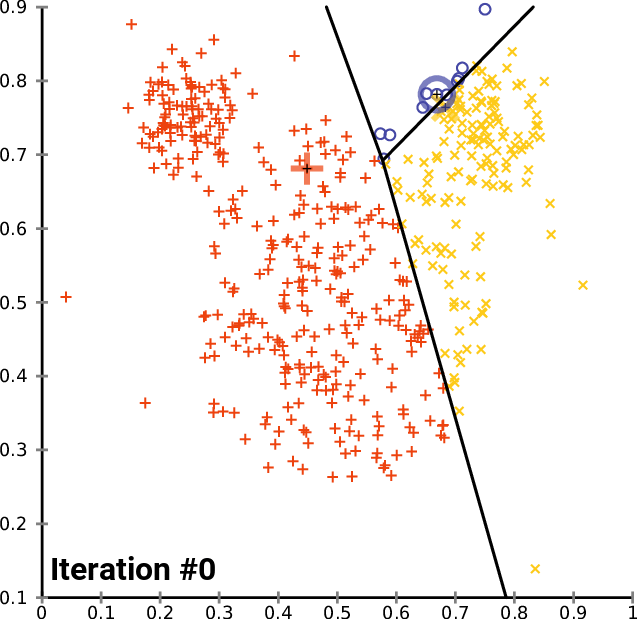
Visualization
Link:
- Kaggle Notebook on Visualizing High Dimensional Clusters
- Visualizing the clusters article
It seems like this algorithm is used quite a lot!
- Poker hand clustering
- Object Detection for Anchor Boxes size clustering
- Image Segmentation to downsample an image to colours
The k-means clustering algorithm divides the training set into different clusters of examples that are near each other.
The K-means algorithm works in three steps:
- Specify the number of clusters provided by algorithm
- Initialize centroids by first shuffling the dataset and then randomly selecting data points for the centroids without replacement.
- Iterate until centroids don’t change by :
- Compute sum of Squared Distance between data points and all centroids.
- Allocate each data point to the cluster that is closest to the others (centroid).
- Set new centroids to be average of the all data points that belong to a given cluster
One of the big issues is bad centroid values because it highly depends on initialization. In practice, you do various trials of K-Means Clustering, and select the trial with the lowest variance for the centroids.
Time complexity? https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
Distance Metrics
Why EMD vs. simpler metrics like Euclidean Distance? See this Stackoverflow thread.
K-Means++
Instead of choosing initial cluster centres randomly, we choose them in a smart way.
Tricks
Use the Triangle Inequality for speedup: https://www.researchgate.net/publication/2480121_Using_the_Triangle_Inequality_to_Accelerate_K-Means
Determining the number of Clusters
At first, for my Poker AI project, I thought I could just take the number that they worked with. But there are some techniques that allows me to compute the optimal number of clusters:
- Elbow method
- Average silhouette method
- Gap statistic method
Extra Resources
- https://www.cs.rice.edu/~as143/COMP642_Spring22/Scribes/Lect15
- https://towardsdatascience.com/k-means-clustering-algorithm-applications-evaluation-methods-and-drawbacks-aa03e644b48a
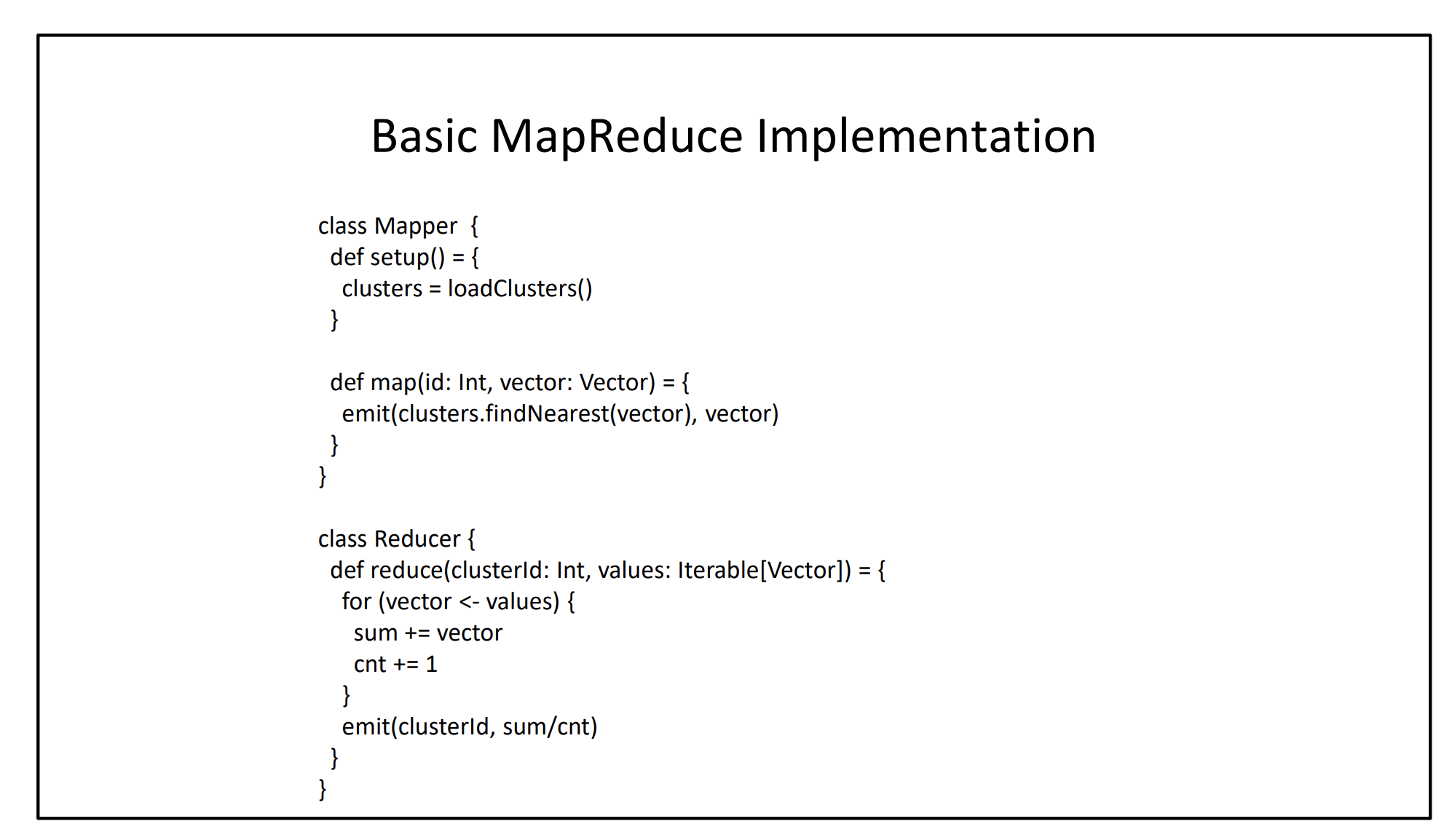
In Spark Shown in CS451