Model-Free Learning

Temporal-Difference Learning

Intuition: Don’t wait until the end of every episode each time to update. Only wait until the next time step.

• TD learns from incomplete episodes, by Bootstrapping
• TD updates a guess towards a guess

Because of this, unlike the Monte-Carlo Learning,

• TD can learn before knowing the final outcome
• TD can learn without the final outcome

TD exploits the MDP structure.

TD Policy Evaluation

Goal: learn $v_{\pi }$ online from experience under policy $\pi$

Simplest TD learning algorithm TD(0): Update value $V(S_t$) towards the TD Target ($R_{t+1}+\gamma V(S_{t+1})$) $V(S_t)=V(S_t)+\alpha {\delta }_t$ where $\delta$ is the TD error between the estimated returns: ${\delta }_t=(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)$

Notice the similarity/difference with Monte-Carlo Learning. We just replace $G_t$ with the Bellman Expectation Backup, $G_t=R_{t+1}+\gamma V(S_{t+1})$. Because we do this, the problem has to be MDP. This isn’t mandatory for Monte-Carlo.

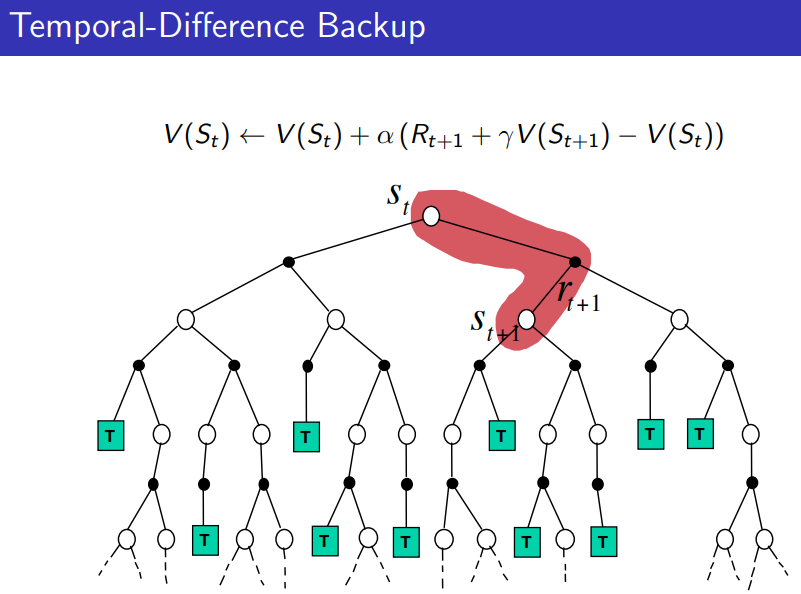
How a TD backup looks like:

TD($\lambda$)

Combines the best out of both world. See Bias - Variance Tradeoff.

TD( \lambda) \neq taking the \lambda-step return

Forward TD-($\lambda$)looks most similar to $\lambda$-step return, however $\lambda$-return is not quite n-step Reinforcement Learning.

The λ-return $G_t^{\lambda }$ combines all n-step returns $G_t^{(n)}$ using weight $(1-\lambda ){\lambda }^{n-1}$ $G_t^{\lambda }=(1-\lambda ){\sum }_{n=1}^{\infty }{\lambda }^{n-1}{G}_t^{(n)}$

You combine all returns into this sort of geometric sum.

You use geometric weighting so the cost is the same as computing TD(0).

There is a forward view and backward view version. Forward-view TD(λ) $V(S_t)\leftarrow V(S_t)+\alpha (G_t^{\lambda }-V(S_t))$

Backward-View TD($\lambda$) Keep an Eligibility Trace for every state $s$. $V(s)\leftarrow V(s)+\alpha {\delta }_t{E}_t(s)$

No one talks about td-lambda nowadays?

In deep RL, TD(λ) is rarely used directly, because:

• Neural networks already provide generalization, so the forward-view λ-return trick doesn’t provide the same advantage as in tabular settings.

Related

• Temporal-Difference Control