Head-to-Head Autonomous Racing

FormulaZero: Distributionally Robust Online Adaptation via Offline Population Synthesis

This is a summary of the paper by Hongrui Zheng, and criticism about how we can work on this to make improvements.

Code

• Source: https://github.com/travelbureau/f0_icml_code
• This repo is also cited: https://github.com/pnorouzi/rl-path-racing

Concepts to be familiar with

• Reinforcement Learning
  • Robust Reinforcement Learning
  • Adversarial Reinforcement Learning
  • POMDP
• Planning in Belief Space
• Distributionally Robust Optimization (DRO)
• Multi-Armed Bandit
• Quality-Diversity Algorithms
• Simulated Tempering
• Determinantal Point Process (DPP)
• Markov Chain Monte-Carlo (MCMC)
• masked Autoregressive Flow (MAF)
• entropic Bregman divergence
• Annealing

The main insights of this paper is thinking about how we can formalize Head-to-Head Autonomous Racing. When it comes to Pure Pursuit (1 car trying to get the fastest lap time), the racing problem has essentially been solved by modelling the dynamics of the racetrack + car and doing Optimal Control (see Raceline Optimization). We have an exact solution (racing line + velocity at each point of the racing line)

However, when it comes to Head-to-Head Autonomous Racing (2+ cars simultaneously racing trying to get the fastest lap time) , it is very difficult to obtain an optimal solution, since we don’t know in advance the behavior of the opponent. We need different Policys for different kinds of opponents.

Why can't you just follow the optimal racing line all the time (i.e. use a policy that follows the Optimal Raceline)?

A simple idea of a solution for Head-to-Head Autonomous Racing would be to always try to follow the optimal racing line. If there is a car in front of you, treat it as an obstacle and perform local planning (ex: using MPC) to go around it.

• NO, see Raceline Optimization. It’s not so simple. There is attacking and defending that you need to think about. In a close battle, both drivers never follow the optimal racing line if they want to drive “optimally”.

Criticism

• In this paper, they treat the opponent as a weighted combination of various profiles of opponents. Why not just directly learn the behaviour of the opponent? Therefore predict its trajectory. Drivers are pretty consistent with the lines they take. And if they are defending, they will take particular line. I think there are 3 driving styles:
  • Pure pursuit (follow optimal racing line)
  • Attacking
  • Defending
• Getting these vehicles to learn what is allowed and not allowed is not something discussed
• This paper doesn’t really explore the concepts of overtaking and defending, which I believe key in racecraft, and building a superhuman autonomous racing agent. Curriculum Reinforcement Learning paper does overtaking, not defending.

Paper Summary

There are two parts of this paper:

1. A method to generate a population of different kinds of opponents that you can play against (“a novel population-based self-play method to parametrize opponent behaviors”)
2. Learning the behaviour of opponent as we race and doing online Optimization to maximize performance (” a provably efficient approach to estimate the ambiguity set and the robust cost online”)

A demonstration with results is also shown at the end of the paper. They provide convergence results that highlight tradeoffs of performance and robustness with respect to these budgets.

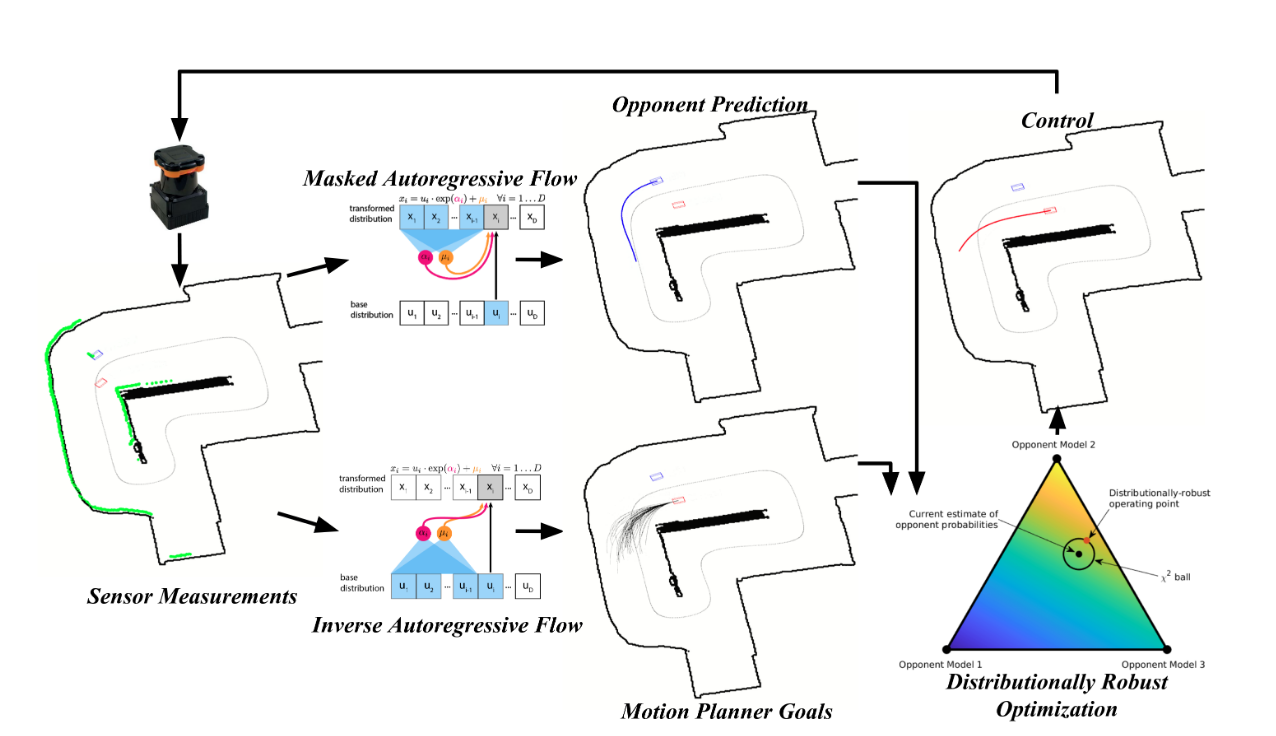
Formalization

We formulate problem as a Robust RL problem, analyzing the system as a POMDP, where the goal is to maximize the expected discounted sum of rewards. The objective is to $\text{maximize}{\inf }_{P_{sa}\in P}{\sum }_t{\lambda }^t\mathbb{E}[r(o(t))]$

• $P$ is the ambiguity set $P$ for the state-action transitions, it captures uncertainty in behaviours of other agents

So how do you parametrize the ambiguity set $P$?

• Rather than directly consider the continuous action space of throttle and steering outputs, we synthesize a library of “prototype” opponent behaviours offline using population-based Self-Play.

• Robustness: When racing against a particular opponent, the agent maintains a belief vector $w(t)$ of the opponent’s behaviour patterns as a categorical distribution over these prototype behaviours. We then parametrize the ambiguity set as a ball around this nominal belief $w(t)$.

• Since you have the ambiguity set, you can now frame it as an optimization problem

Final planning is done in belief space, the inspiration comes from Distributionally Robust Optimization, that is, coming up with robust solutions of optimization problems affected by uncertain probabilities.

Population Synthesis (Offline)

Step 1: Parametrized policy

1. Goal Generator: Inverse autoregressive flow weights
2. Goal Evaluator: Non-differentiable cost function weights

You start with random configurations of $\theta$ (NN parameters) and $x$ (cost weights at the top. 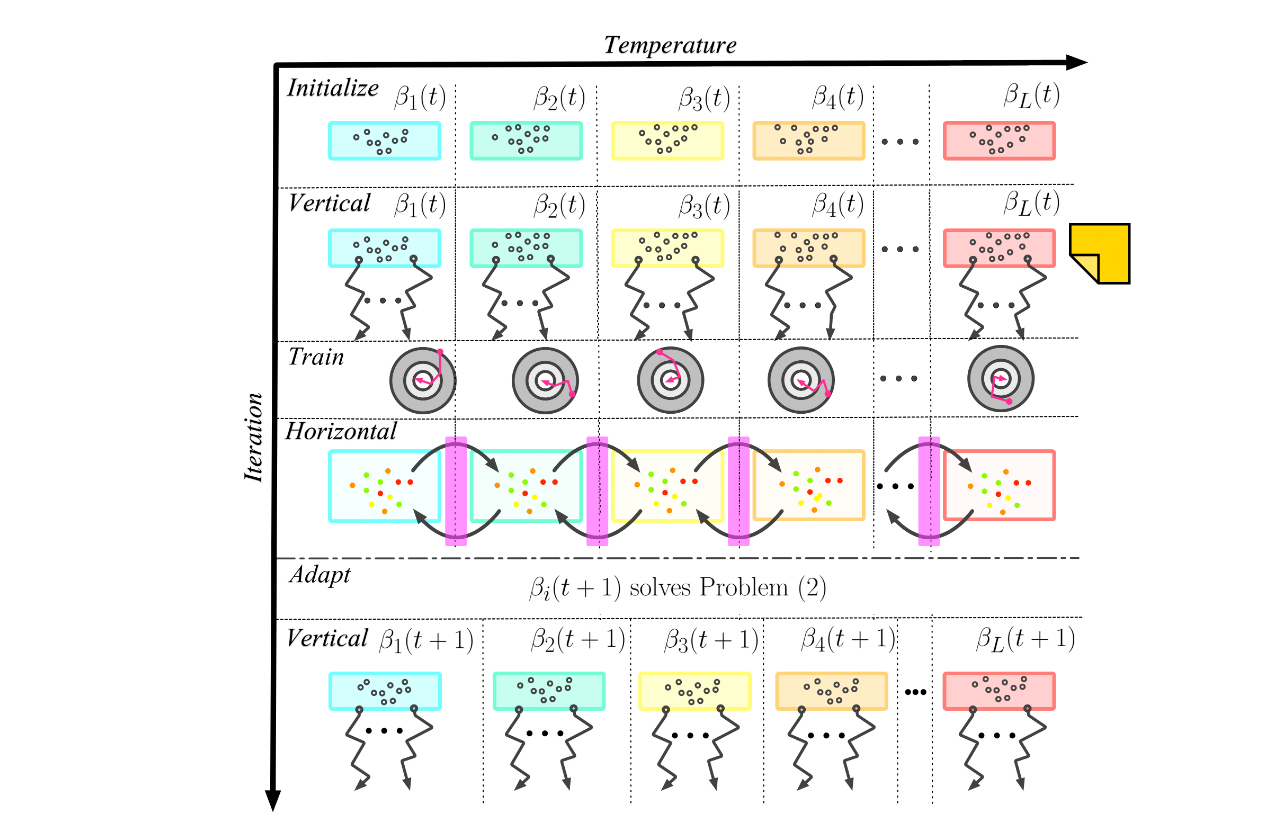The colors represent the various temperatures.

• Blue = only accepts changes to configurations which improve performance (exploitation)
• Red = accepts any configuration change regardless of performance (exploration)

Online Adaptation

You approximate the robust cost because there are many opponents. At each time step we sample N < d opponent prototypes. You belief distribution initializes in Uniform Distribution.

To match to the opponent, they frame it as a Multi-Armed Bandit problem. They update their belief vector $w(t)$ using a modified EXP3 Algorithm.

$\frac{\rho }{N_W}$ (you can think of this as the radius of the ball around the point in the triangle). The greater that value, the great the TTC, it’s more robust but you are farther from the opponent.

More aggressive

Personal Notes

Random things jotted down.

Questions

1. I want him to go more into Population synthesis, and how those parametrized policies are generated. And I don’t understand his ADAPT algorithm works
2. I think he had this diagram split into 2 parts
   1. Masked Autoregressive Flow (for opponent prediction)
   2. Inverse Autoregressive Flow (to generate your own opponent)
3. Population synthesis
   1. Why is the vertical non-differentiable?
      1. And then train is differentiable?
   2. How do the temperatures change?
4. Actual racing → I don’t understand how the ego car comes up with a $\theta$, does it just use the highest one from the offline population synthesis?
   1. And I don’t understand where the Autoregressive Flow comes into play
5. Training 100 iterations for population synthesis, it’s around 3 seconds per iteration
6. Did they use the same track?
   1. You need to retrain everything when you have a new track, because the cost weights $x$ are going to be very different
7. Sim2Real problem?
8. So no adaptation is how? You just take the sample generated from the sample that has the lowest $f(x,\theta )$
9. So how does the car actually drive? There are a bunch of goal posts. You use a Clothoid
   1. They have a lookup table

Simulation, have them play head to head. Each of the dot represents one racing variant. Use MCMC because this is the non-differentiable function.

Generate from a Boltzmann Distribution. you have an operating point about your belief (remember this triangle). In Belief Space Planning, you would only plan according to that one point in the triangle.

We try to minimize the worst case cost. Use a ${\chi }^2$ ball.

We want to sample pairs $(x,\theta )$ where

• $x$ is a weighting of various cost functions for the trajectories
• $\theta$ are parameters of a Neural Net to represent a sample trajectory to follow using the Normalizing Flow

They use a differentiable function $f(x,\theta )$ where $f$ is the simulated lap time, and our goal is to minimize $f$.

It’s so weird, they are taking all these concepts from Materials Science with temperature in order to model Stochasticity.

They use something called AADAPt, which buildings upon replica-exchange MCMC, you can learn more about it here. It is a standard approach to maintaining a population of configurations