Model Predictive Control
Model Predictive Control (MPC) is a control strategy that uses a model of the environment, and can thus can predict future behavior, to optimize the control action to be applied over several time steps.
Why is MPC better than a Stanley Controller?
Stanley is a reactive method, because it simply reacts to the distance to the horizontal distance. The limitations are talked about through the Cyrill course (see notes before)
Links:
- https://roboticsknowledgebase.com/wiki/actuation/model-predictive-control/
- https://david010.medium.com/vehicle-mpc-controller-33ae813cf3be
- OP Repo? https://github.com/matssteinweg/Multi-Purpose-MPC
- F1TENTH MPC Lab: https://github.com/f1tenth/f1tenth_lab9_template
To solve MPC, we can do Quadratic Programming.
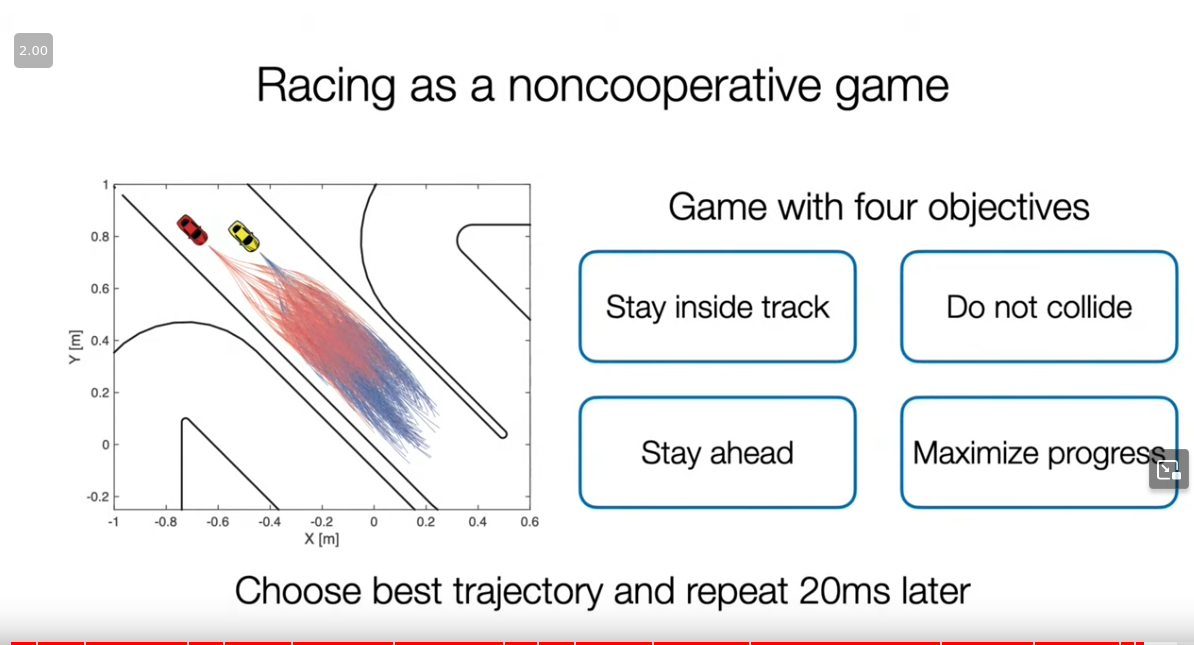
One of the really cool things we can do with MPC is this: https://www.youtube.com/watch?v=JoHfJ6LEKVo&ab_channel=IfAETHZurich
This stuff is complicated, but really interesting. If you want to be the best engineer in the world, this is the kind of stuff you need to understand.
Data-Driven MPC: https://arxiv.org/pdf/2102.05773.pdf really interesting work with drones.
Reinforcement Learning techniques are model-free.
MPC is NOT multiple PIDs stacked?
Well yea obviously, MPC is about having a model of the dynamics, and then sampling trajectories.
Notes from Cyrill Class
- Model Predictive Control - Part 1: Introduction to MPC (Lasse Peters)
- Model Predictive Control - Part 2: Numerical Methods for MPC (Lasse Peters)
Part 1
Limitations of Reactive Control
- Non-trivial for more complex systems
- Control gains must be tuned manaully
- Separation into longitudinal and lateral controllers ignores coupling
- No handling of constraints such as obstacles
- Ignore future decisions
Therefore, we have optimal control: how to best control the system?
- Optimal Control is framing control as an optimization problem.
- Optimal control: Model We need to have a model of the system dynamics, so that we can predict the evolution of the state for a given sequence of inputs.

Typically, solving the optimization problem has no closed-form solution.
MPC adds the idea of receding horizon control.
MPC design is a tradeoff in choice of model family: model accuracy vs. complexity
This is super cool, they use MPC to solve head to head racing??